With Luis Silvestre and Cédric Villani, we proved that the Fisher information decreases along the flow of the space-homogeneous Boltzmann equation for a large class of collision kernels including the most classical ones.
With Amélie Loher, we wrote and uploaded to hal and arxiv a preprint entitled Conditional appearance of decay for the non-cutoff Boltzmann equation in a bounded domain.
Abstract: This work is concerned with the appearance of decay bounds in the velocity variable for solutions of the space-inhomogeneous Boltzmann equation without cutoff posed in a domain in the case of hard and moderately soft potentials. Such bounds are derived for general non-negative suitable weak subsolutions. These estimates hold true as long as mass, energy and entropy density functions are under control. The following boundary conditions are treated: in-flow, bounce-back, specular reflection, diffuse reflection and Maxwell reflection. The proof relies on a family of Truncated Convex Inequalities that is inspired by the one recently introduced by F. Golse, L. Silvestre and the first author (2023). To the best of our knowledge, the generation of arbitrary polynomial decay in the velocity variable for the Boltzmann equation without cutoff is new in the case of soft potentials, even for classical solutions.
With J. Guerand and C. Mouhot, we uploaded on HAL and arxiv a new preprint entitled Gehring’s Lemma for kinetic Fokker-Planck equations.
Abstract: In this article, we establish a « Gehring lemma » for a real function satisfying a reverse Hölder inequality on all « kinetic cylinders » contained in a large one: it asserts that the integrability degree of the function improves under such an assumption. The kinetic cylinders are derived from the non-commutative group of invariances of the Kolmogorov equation. Our contributions here are (1) the extension of Gehring’s Lemma to this kinetic (hypoelliptic) scaling used to generate the cylinders, (2) the localisation of the lemma in this hypoelliptic context (using ideas from the elliptic theory), (3) the streamlining of a short and quantitative proof. We then use this lemma to establish that the velocity gradient of weak solutions to linear kinetic equations of Fokker-Planck type with rough coefficients have Lebesgue integrability strictly greater than two, while the natural energy estimate merely ensures that it is square integrable. Our argument here is new but relies on Poincaré-type inequalities established in previous works.
With F. Golse and Luis Silvestre, we uploaded a new paper entitled: Partial regularity in time for the space-homogeneous Boltzmann equation with very soft potentials. HAL | arxiv
Summary: We prove that the set of singular times for weak solutions of the homogeneous Boltzmann equation with very soft potentials constructed as in Villani (1998) has Hausdorff dimension at most |γ+2s|/2s with γ∈[−4s,−2s) and s∈(0,1).
With Nicolas Forcadel et Régis Monneau, we recently uploaded on HAL and arxiv two new preprints about Hamilton-Jacobi equations.
The first one is interested in the understanding of viscosity solutions for HJ equations posed on a domain. This theory allows one to easily construct weak solutions for boundary value problems. These weak viscosity solutions can be studied thanks to the relaxation operator introduced by J. Guerand. In this new work, a link with classical Godunov fluxes is exhibited. As an application, the classical Neumann and Dirichlet problems are discussed.
The second one is interested in uniqueness of viscosity solutions. We elaborate on a method introduced by P.-L. Lions and P. Souganidis to prove new comparison principles for HJ equations posed on a domain. We follow them by performing a blow analysis and by reducing to a 1D problem but we depart from their method by blowing up the sub-solution and the super-solution simultaneously.
With F. Golse and A. F. Vasseur, we uploaded a new preprint about local regularity estimates for the Landau equation with very soft potentials.
Reference. F. Golse, C. Imbert and A. F. Vasseur. Local regularity for the space homogeneous Landau equation with very soft potentials. hal | arxiv
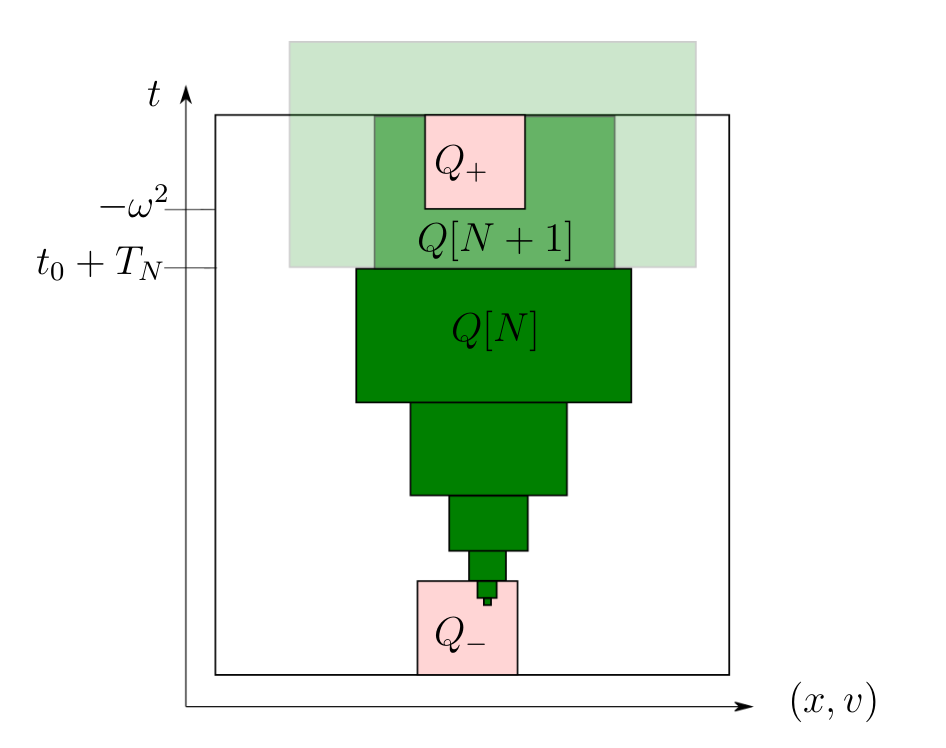
We just posted online with Jessica Guerand a new preprint entitled Log-transform and the weak Harnack inequality for kinetic Fokker-Planck equations. It is available on HAL and on arxiv.
Abstract: This article deals with kinetic Fokker-Planck equations with essentially bounded coefficients. A weak Harnack inequality for non-negative super-solutions is derived by considering their Log-transform and following S. N. Kruzhkov (1963). Such a result rests on a new weak Poincaré inequality sharing similarities with the one introduced by W. Wang and L. Zhang in a series of works about ultraparabolic equations (2009, 2011, 2017). This functional inequality is combined with a classical covering argument recently adapted by L. Silvestre and the second author (2020) to kinetic equations.
Together with Luis Silvestre (University of Chicago), we wrote a survey article about a series of works we recently completed about the Boltzmann equation. See hal and arxiv.
The Boltzmann equation is a nonlinear partial differential equation that plays a central role in statistical mechanics. From the mathematical point of view, the existence of global smooth solutions for arbitrary initial data is an outstanding open problem. In the present article, we review a program focused on the type of particle interactions known as non-cutoff. It is dedicated to the derivation of a priori estimates in C∞, depending only on physically meaningful conditions. We prove that the solution will stay uniformly smooth provided that its mass, energy and entropy densities remain bounded, and away from vacuum.
I wrote with Luis Silvestre (University of Chicago) a series of articles about the Boltzmann equation without cut-off in the inhomogeneous case. The goal was to prove C∞ a priori estimates for solutions of the inhomogeneous Boltzmann equation without cut-off, conditional to point-wise bounds on their mass, energy and entropy densities.
The final paper is entitled Global regularity estimates for the Boltzmann equation without cut-off.
It relies on the L∞ estimate derived by Luis Silvestre (see this paper), the local Hölder estimate derived in this paper, the Schauder estimate for kinetic equations with integral diffusion derived in this paper and the pointwise decay estimates for large velocities derived in this paper with Clément Mouhot and Luis Silvestre.
In collaboration with F. Golse, M. P. Gualdani and A. F. Vasseur. It can be found in the hal and also in arxiv.
Abstract: We prove that the set of singular times for weak solutions of the space homogeneous Landau equation with Coulomb potential constructed as in [C. Villani, Arch. Rational Mech. Anal. 143 (1998), 273-307] has Hausdorff dimension at most 1/2.