We just posted online with Jessica Guerand a new preprint entitled Log-transform and the weak Harnack inequality for kinetic Fokker-Planck equations. It is available on HAL and on arxiv.
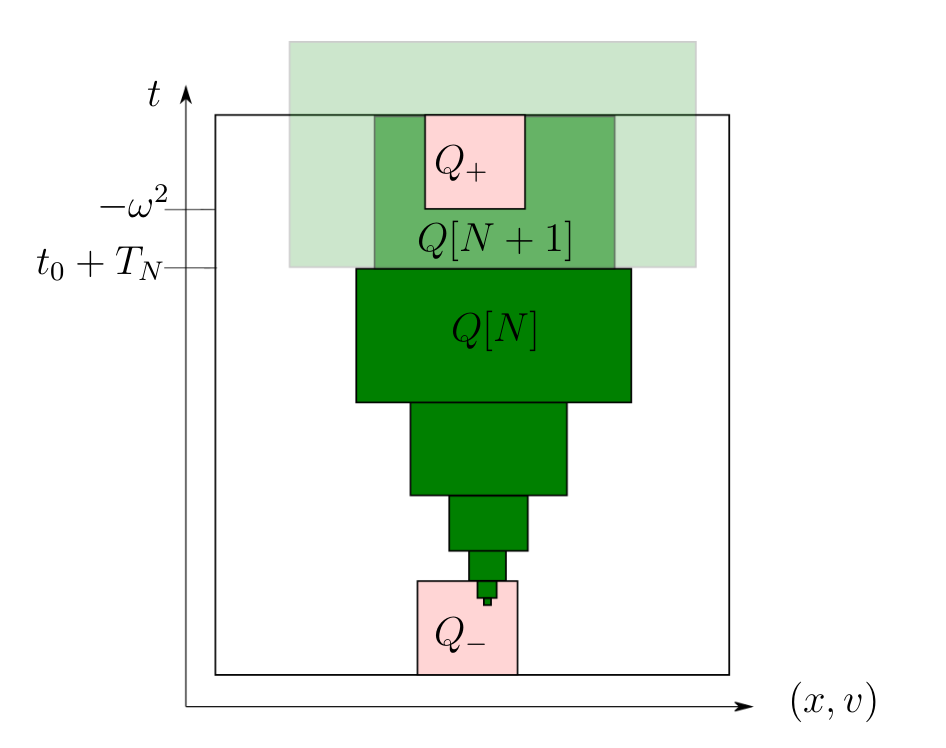
Abstract: This article deals with kinetic Fokker-Planck equations with essentially bounded coefficients. A weak Harnack inequality for non-negative super-solutions is derived by considering their Log-transform and following S. N. Kruzhkov (1963). Such a result rests on a new weak Poincaré inequality sharing similarities with the one introduced by W. Wang and L. Zhang in a series of works about ultraparabolic equations (2009, 2011, 2017). This functional inequality is combined with a classical covering argument recently adapted by L. Silvestre and the second author (2020) to kinetic equations.