With Amélie Loher, we wrote and uploaded to hal and arxiv a preprint entitled Conditional appearance of decay for the non-cutoff Boltzmann equation in a bounded domain.

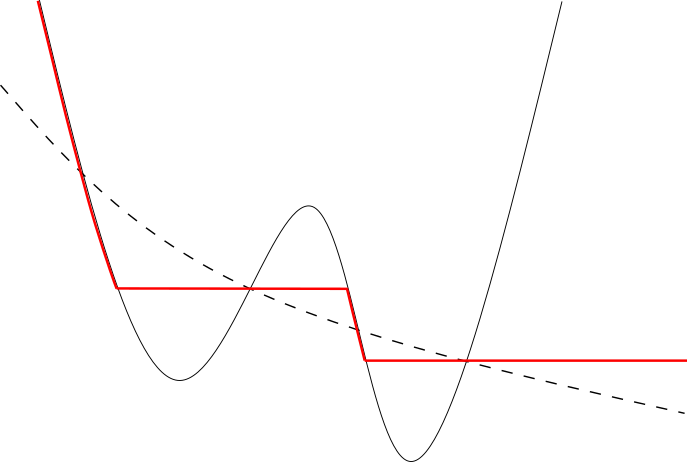
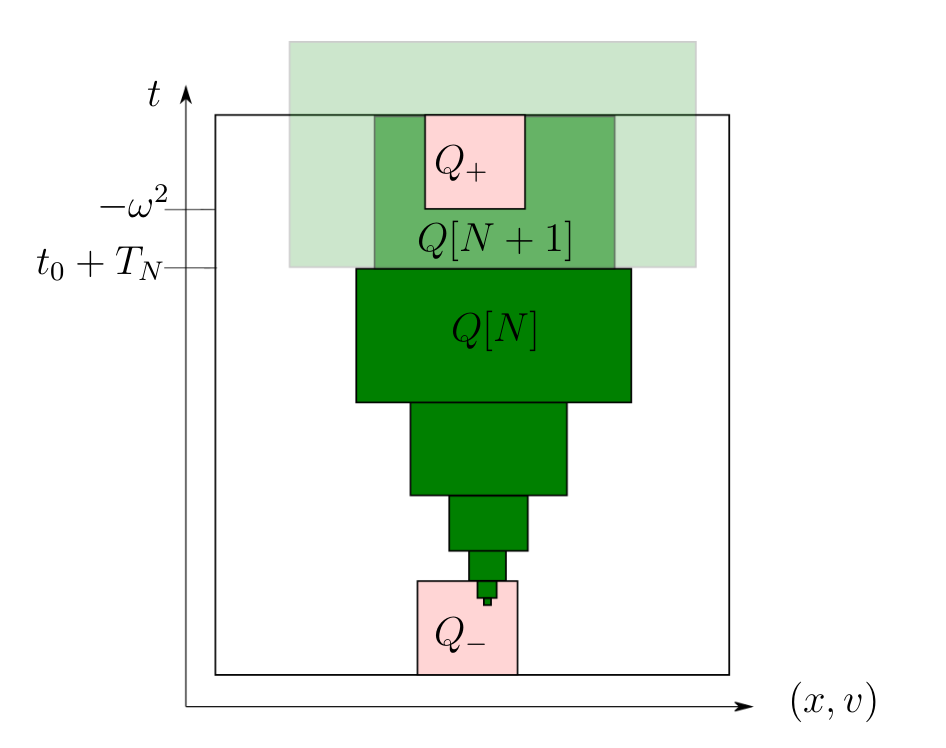
Abstract: This work is concerned with the appearance of decay bounds in the velocity variable for solutions of the space-inhomogeneous Boltzmann equation without cutoff posed in a domain in the case of hard and moderately soft potentials. Such bounds are derived for general non-negative suitable weak subsolutions. These estimates hold true as long as mass, energy and entropy density functions are under control. The following boundary conditions are treated: in-flow, bounce-back, specular reflection, diffuse reflection and Maxwell reflection. The proof relies on a family of Truncated Convex Inequalities that is inspired by the one recently introduced by F. Golse, L. Silvestre and the first author (2023). To the best of our knowledge, the generation of arbitrary polynomial decay in the velocity variable for the Boltzmann equation without cutoff is new in the case of soft potentials, even for classical solutions.