This note is a comprehensible summary of the article Numerical study of a viscous breaking water wave and the limit of vanishing viscosity (joint work with Emmanuel Dormy, J. Fluid Mech. Rapids, 2024), written to be comprehensible by non-scientific people.
I. What are we talking about?
Wave breaking is a well-known natural phenomenon (figure 1). However many things related to this phenomenon are yet to be understood.

In this paper, we describe a new numerical methods to solve the equations of fluid mechanics to investigate an example of breaking wave. Particular emphasis is put on the effects of viscosity on the overall shape of the wave.
II. The equations of fluid mechanics
One of the most celebrated equation of fluid mechanics is called the Navier-Stokes equation, \[ \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}\cdot\nabla)\mathbf{u} = -\nabla p + \frac{1}{\mathrm{Re}}\cdot\Delta\mathbf{u} + \mathbf{g} \] \[ \nabla\cdot\mathbf{u} = 0 \] It describes surprisingly well the behavior of a fluid (liquid or gas), from the water flow coming out of a faucet to the formation of planetary storms. However it is impossible to solve it in most of the interesting cases...
A way to bypass this (huge) limitation in order to still get scientific knowledge from this equation is to use computers. Even though they are not able to solve it aswell, their computational power can be used to approximate the solution. We call this carrying out a numerical study. This is precisely what we have done in this work: solving numerically the Navier-Stokes equation in the case of a breaking wave.
III. Viscosity
In the Navier-Stokes equation shown above, there is a number \(\mathrm{Re}\), called the Reynolds number. It tells how viscous the fluid considered is. When it is large, the fluid is not very viscous (like water or air) while when it is small, the effects of viscosity become prevailing (as in honey).
At ambient temperature, the viscosity of water is almost identical everywhere, and very small. However, considering large-scale phenomena (e.g. small water waves) also decreases the Reynolds number (hence makes the viscosity more important). In our study, we have been interested in the behavior of the wave as we increase the Reynolds number. A comparison of water waves with different values of \(\mathrm{Re}\) is shown in figure 3 (cover of this article).
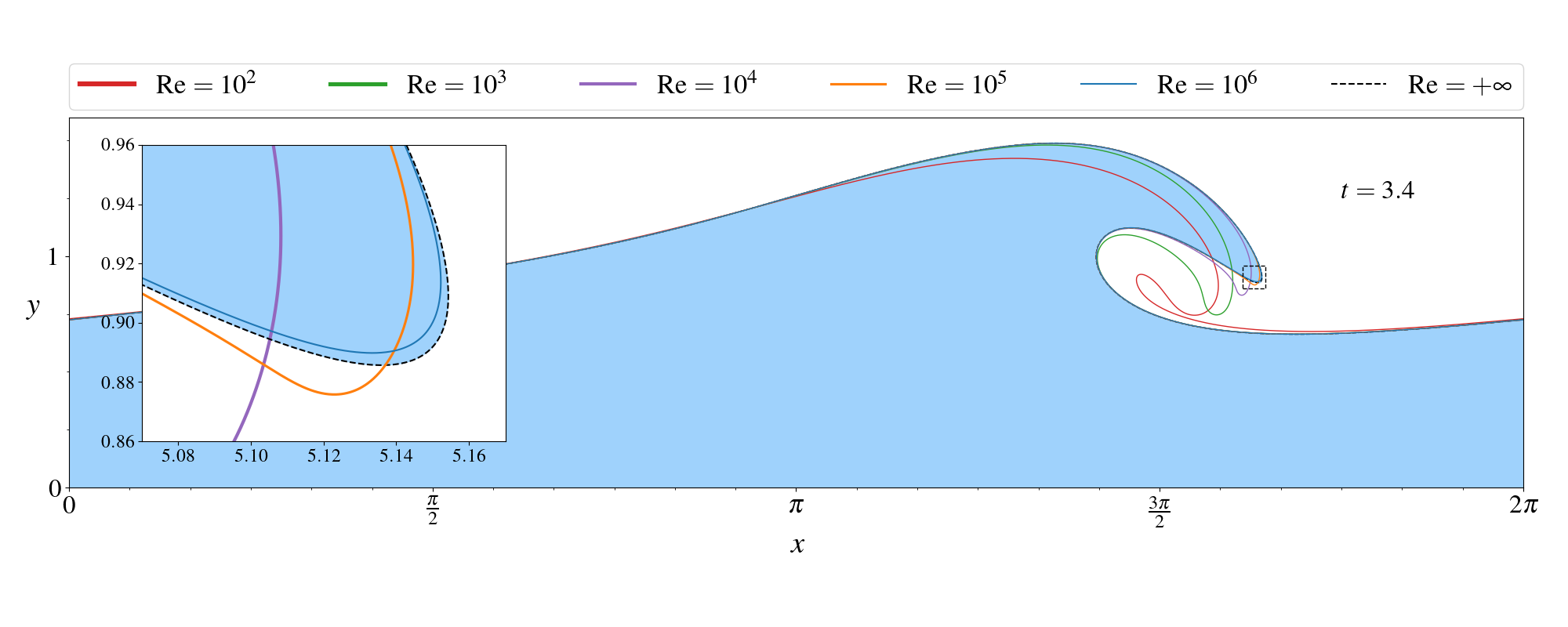
We see that, as the Reynolds numer is increased (i.e. as the viscosity becomes less important, as is the case for a water wave on a beach), the crest of the wave tends to become sharper until it reaches a limit.
This observation has lead us to conclude that the effects of viscosity are not negligible only in regions where the size of the crest, let us call it \( s \), is comparable or smaller than the inverse square-root of the Reynolds number, so only if \[ s \approx \frac{1}{\sqrt{\mathrm{Re}}} \]
IV. Boundary layer
The general effect of viscosity in fluid mechanics is that is dissipates energy. In order to know where this energy dissipation happens in the water, we represent it in figure 4.
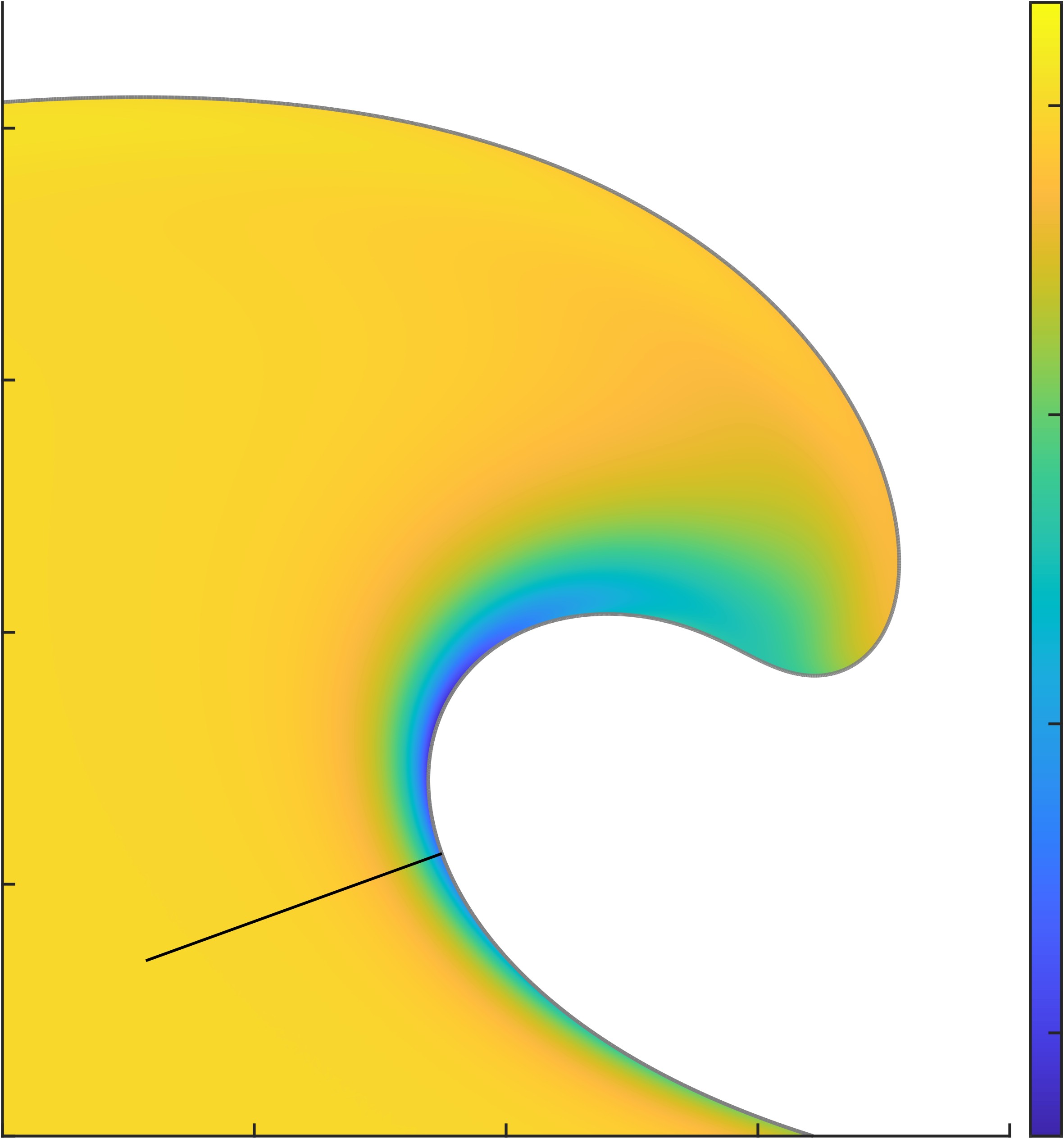

The energy dissipation diagram shown in figure 4 shows a structure confined in the vicinity of the water-air interface. This is called a boundary layer. Notice that as the Reynolds number increases, the boundary layer size decreases. Such layer of energy dissipation has already been observed but was not extensively investigated before.
This boundary layer is negligible in the case of a breaking wave. However it is reasponsible for amplitude dumping of traveling water waves far from the shore (about 10% of the amplitude for a wave traveling a thousand kilometers).
V. Conclusion
We have developped a new approach to solve the equations of fluid mechanics in order to investigate breaking waves. This method has been used to extensively characterise the effects of viscosity on the shape of a wave.
There is still a formidable amount of questions to be adressed in future studies using this code.