Nous proposons ici un résumé compréhensible de l'article Numerical study of a viscous breaking water wave and the limit of vanishing viscosity (Étude numérique d'une vague océanique déferlante et de la limite de faible viscosité, travail commun avec Emmanuel Dormy, J. Fluid Mech. Rapids, 2024), écrit pour un public non-scientifique.
I. De quoi parlons-nous ?
Le déferlement des vagues océaniques est un phénomène naturel bien connu (figure 1). Cependant, encore aujourd'hui un grand nombre de questions en lien avec ce dernier échappent à la compréhension des scientifiques.

Dans cet article, nous proposons une nouvelle méthode numérique pour résoudre les équations de la mécanique des fluides afin d'étudier un exemple de déferlante. Les effets de la viscosité sur la forme de ma vague sont particulièrement mis en exergue.
II. Les équations de la mécanique des fluides
L'équation la plus connue de la mécanique des fluides est incontestablement l'équation de Navier-Stokes, \[ \frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u}\cdot\nabla)\mathbf{u} = -\nabla p + \frac{1}{\mathrm{Re}}\cdot\Delta\mathbf{u} + \mathbf{g} \] \[ \nabla\cdot\mathbf{u} = 0 \] Elle décrit incroyablement bien la façon dont se comporte un fluide (liquide ou gaz), que ce soit de l'eau coulant depuis un robinet ou la formation d'une tempête. Cependant, il est impossible de la résoudre dans les cas les plus intéressants...
La façon la plus commune de contourner ce problème est d'utiliser des ordinateurs pour tout de même étudier cette équation. Même si ces derniers sont aussi peu capables de la résoudre que nous, il leur est possible de calculer une approximation de la solution. Nous appelons cela une étude numérique. Il s'agit exactement de ce que nous avons accompli dans cet article : étudier numérique l'équation de Navier-Stokes dans le cas d'une vague déferlante.
III. Viscosité
Dans l'équation de Navier-Stokes, présentée plus haut, il y a un nombre, \(\mathrm{Re}\), appelé le nombre de Reynolds. Il nous explique à quel point les effets visqueux sont importants dans le fluide. Lorsque \(\mathrm{Re}\) est grand, ils sont négligeables (comme dans le cas de l'eau ou de l'air) alors que lorsqu'il est petit, la viscosité joue un rôle prépondérant (comme dans du miel).
À température ambiente, la viscosité de l'eau est très petite et partout la même. Par contre, si l'on se met à considérer des phénomènes à grande échelle (e.g. de petites vagues), l'importance des effets visqueux augmente, si bien que le nombre de Reynolds diminue. Dans notre étude, nous avons essayer de quantifier les effets d'une augmentation du nombre de Reynolds (ce qui peut être interprété comme une augmentation de la taille de la vague) sur la forme de la crête de la vague. Une comparaison des vagues pour différentes valeurs de \(\mathrm{Re}\) est visible en figure 3 (couverture de cet article).
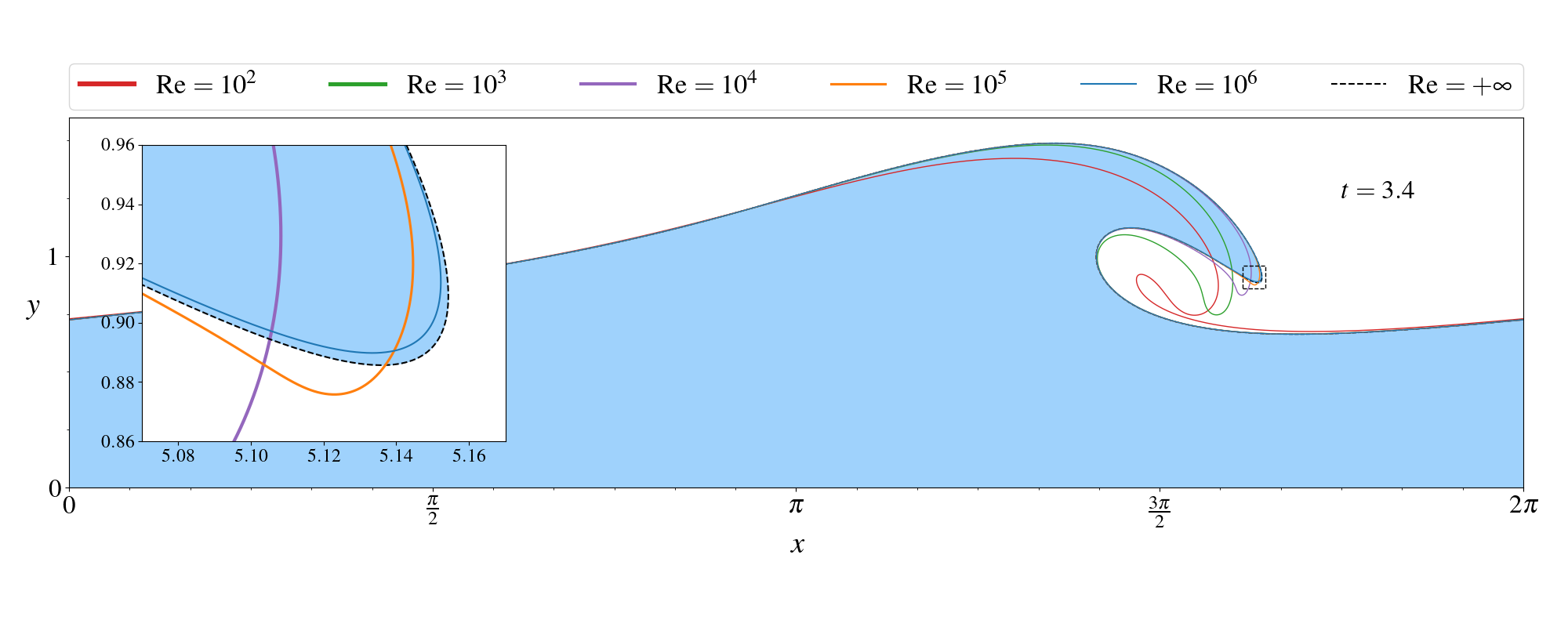
Nous voyons que, alors que nous augmentons la valeur de \(\mathrm{Re}\) (i.e. alors que la viscosité devient de moins en moins importante, comme c'est le cas pour une vague déferlant proche d'une plage), la crête de la vague devient de plus en plus pointue jusqu'à une certaine limite.
Cette observation nous a conduit à penser que les effets de la viscosité ne sont importants que dans les régions où la taille de la crête, appelons-la \(s\), est comparable ou plus petite que l'inverse de la racine carrée du nombre de Reynolds, \[ s \approx \frac{1}{\sqrt{\mathrm{Re}}} \]
IV. Couche limite
En mécanique des fluides, il est connu que l'effet le plus important de la viscosité est qu'elle dissipe de l'énergie. Pour savoir où dans la vague cette dissipation a lieur, nous la représentons en figure 4.
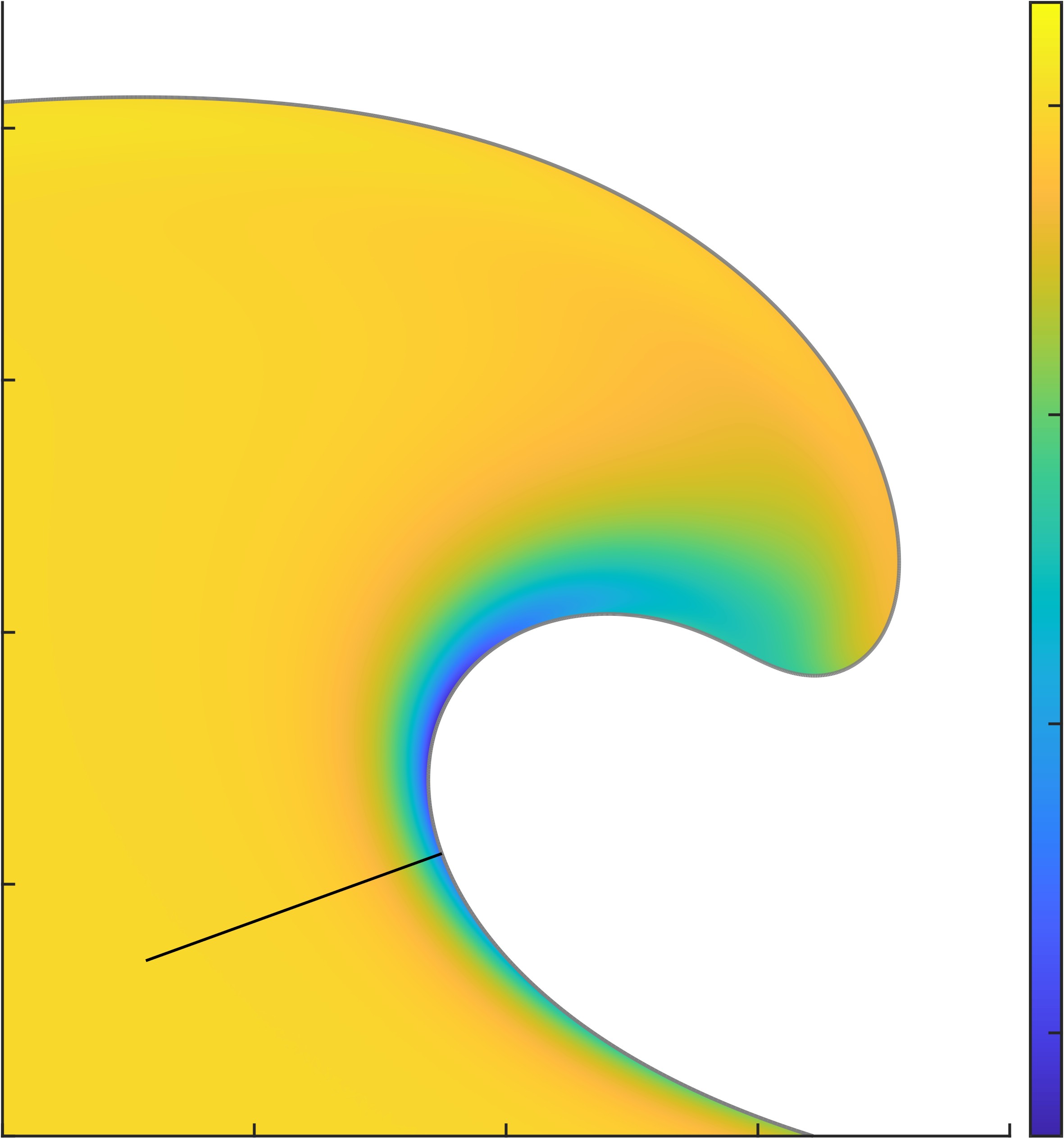

Le diagramme de dissipation d'énergue de la figure 4 montre une structure confinée dans une région proche de l'interface eau-air. Nous appelons cela une couche limite. Remarquons qu'alors que le nombre de Reynolds augmente, la taille de cette couche limite diminue. Cette dernière avait déjà été observée dans des vagues déferlantes mais jamais étudiée en détails.
Cette couche limite est complètement négligeable dans le cas d'une déferlante "réelle" (elle ne mesure que quelques millimètres). Cependant, elle est responsable de la perte d'amplitude d'une vague océanique dans l'océan profond (environ 10% de la taille de la vague est perdu si cette dernière se déplace d'environ 1000 kilomètres).
V. Conclusion
Nous avons développé une nouvelle façon de résoudre les équations de la mécanique des fluides dans le cas d'une vague déferlante. Cette méthode a été employée pour étudier l'influence de la viscosité sur la forme de la vague.
Il reste de très importante questions qui mériteraient que l'on s'y attaque à l'aide de ce code. Cela laisse entrevoir de possibles applications de notre méthode dans des travaux futurs.