| Home |
Research
|
 |
| Home |
Research
|
 |
Operads are tools for encoding algebraic structures. An operad can be seen as a class of abstract operations, equipped with a certain coherent manner to compose them.
 The endomorphism operad
To understand the definition of an operad, one can look at the fundamental example given by the endomorphism operad.
Let `X` be a set. We denote by `End_X(n):= Hom(X^{n}, X)` the set of all maps from the product of `n` copies of `X` to `X`.
An element `f` of `End_X(n)` can be thought as a tree where the number of leaves corresponds to the inputs of `f` and the root to the output.
The following picture corresponds to a map ` f : X^{ n} \to X` of arity `n`.
The endomorphism operad
To understand the definition of an operad, one can look at the fundamental example given by the endomorphism operad.
Let `X` be a set. We denote by `End_X(n):= Hom(X^{n}, X)` the set of all maps from the product of `n` copies of `X` to `X`.
An element `f` of `End_X(n)` can be thought as a tree where the number of leaves corresponds to the inputs of `f` and the root to the output.
The following picture corresponds to a map ` f : X^{ n} \to X` of arity `n`.
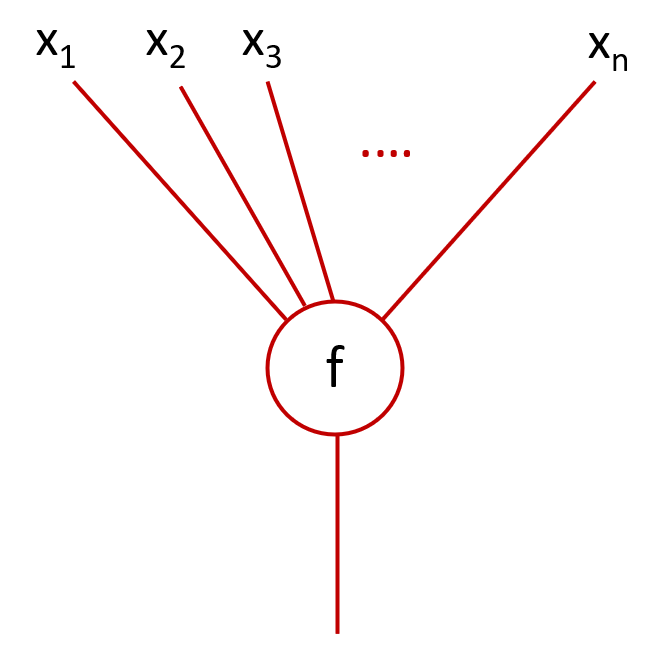 Given `f : X^{ n} \to X` and `g : X^{ m} \to X`, there exists an obvious manner to compose them by replacing
one of the inputs of `f` by the output of `g`. For example, by choosing the second input of `f`, we get
Given `f : X^{ n} \to X` and `g : X^{ m} \to X`, there exists an obvious manner to compose them by replacing
one of the inputs of `f` by the output of `g`. For example, by choosing the second input of `f`, we get
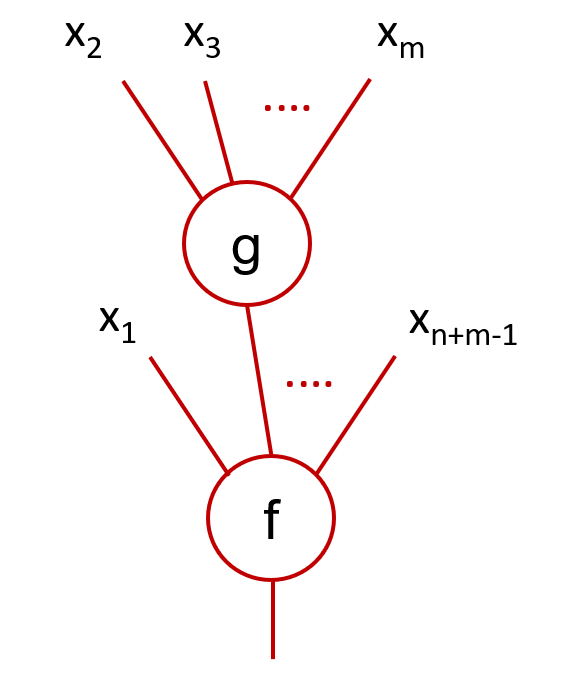 This composition corresponds to the formula `f(x_1,g(x_2, \cdots, x_m), \cdots, x_{n+m-1})`, for all `x_1, \cdots, x_{n+m-1} \in X`.
It is denoted by `f \circ_2 g`. We replaced the second input of `f` but we could have chosen the `i`th input, for each
`i \in \{1, \cdots, n \}`. This leads other compositions that we denote `f \circ_i g`.
If one composes several maps this way, the order of the compositions does not matter.
In other words, the compositions are associative. For instance, given a third map `h : X^{ p} \to X`, one has
`(f \circ_2 g) \circ_4 h = f \circ_2 (g \circ_3 h)` or `(f \circ_2 g) \circ_{n+m-2} h = (f \circ_{n-1} h) \circ_2 g` .
Thus, the two examples of compositions, depicted by the following pictures, are not ambiguous.
This composition corresponds to the formula `f(x_1,g(x_2, \cdots, x_m), \cdots, x_{n+m-1})`, for all `x_1, \cdots, x_{n+m-1} \in X`.
It is denoted by `f \circ_2 g`. We replaced the second input of `f` but we could have chosen the `i`th input, for each
`i \in \{1, \cdots, n \}`. This leads other compositions that we denote `f \circ_i g`.
If one composes several maps this way, the order of the compositions does not matter.
In other words, the compositions are associative. For instance, given a third map `h : X^{ p} \to X`, one has
`(f \circ_2 g) \circ_4 h = f \circ_2 (g \circ_3 h)` or `(f \circ_2 g) \circ_{n+m-2} h = (f \circ_{n-1} h) \circ_2 g` .
Thus, the two examples of compositions, depicted by the following pictures, are not ambiguous.
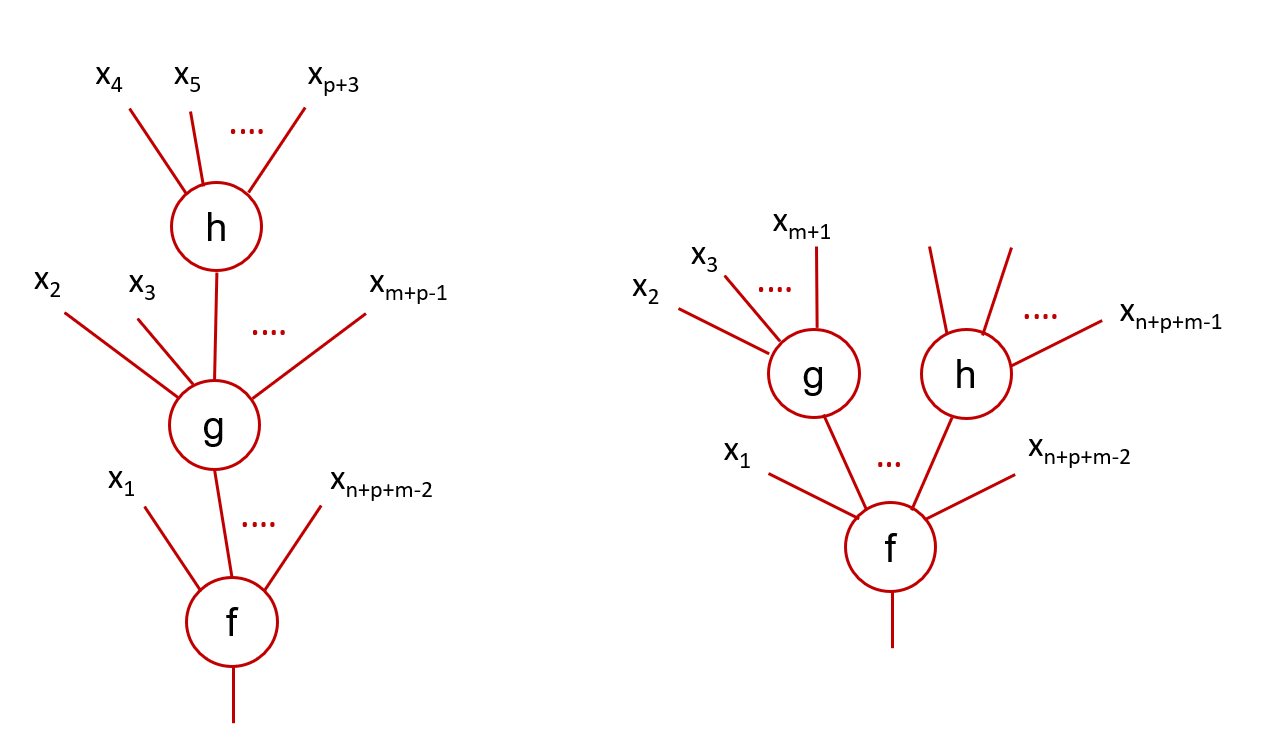 We speak of sequential composition in the case of the left tree and parallel composition in that of the right tree.
The map `id_X \in End_X(1)` is a neutral element, that is, for any `f : X^{ n} \to X` and `i \in \{1, \cdots, n \}` , the composition
`f \circ_i id_X ` is equal to `f` . Similarly, we have `id_X \circ_1 f =f` .
We can also allow maps `X^{ 0} \to X` of arity `0` . In this case, the space `X^{0}` is simply a singleton
and every map `X^{ 0} \to X` is fully determined by the data of one element `a \in X`. Thus, there is an isomorphism `End_X(0) \cong X`.
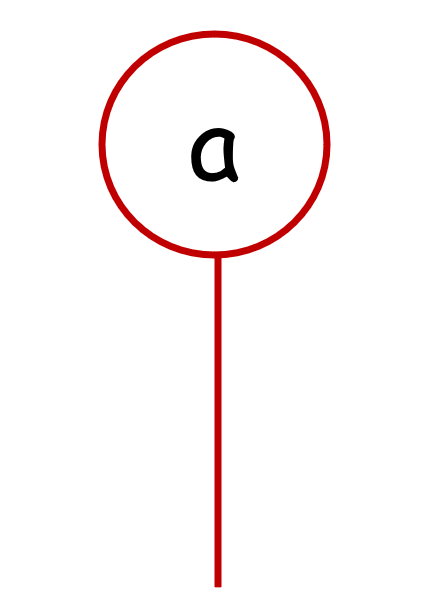
We can depict these maps of arity `0` as corks:
We speak of sequential composition in the case of the left tree and parallel composition in that of the right tree.
The map `id_X \in End_X(1)` is a neutral element, that is, for any `f : X^{ n} \to X` and `i \in \{1, \cdots, n \}` , the composition
`f \circ_i id_X ` is equal to `f` . Similarly, we have `id_X \circ_1 f =f` .
We can also allow maps `X^{ 0} \to X` of arity `0` . In this case, the space `X^{0}` is simply a singleton
and every map `X^{ 0} \to X` is fully determined by the data of one element `a \in X`. Thus, there is an isomorphism `End_X(0) \cong X`.
We can depict these maps of arity `0` as corks:
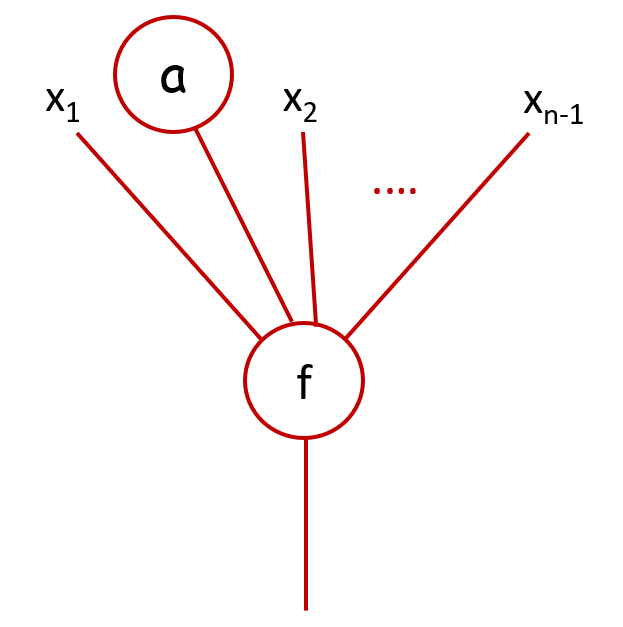
 If `f` is a map `X^{n} \to X` where `n \geq 1`, the composition `f \circ_i a` for `i \in \{1, \cdots, n \}` of `f` with a cork `a \in End_X(0)`
amounts to blocking the input `i` of `f` by forcing it to be equal to `a` . With the tree representation, we obtain the following picture for `f \circ_2 a`
which corresponds to the formula `f(x_1,a,x_2, \cdots, x_{n-1})`, for all `x_1, \cdots, x_{n-1} \in X`.
If `f` is a map `X^{n} \to X` where `n \geq 1`, the composition `f \circ_i a` for `i \in \{1, \cdots, n \}` of `f` with a cork `a \in End_X(0)`
amounts to blocking the input `i` of `f` by forcing it to be equal to `a` . With the tree representation, we obtain the following picture for `f \circ_2 a`
which corresponds to the formula `f(x_1,a,x_2, \cdots, x_{n-1})`, for all `x_1, \cdots, x_{n-1} \in X`.
 We can now give the definition of an operad.
We can now give the definition of an operad.
 Definition of an operad
A (nonsymmetric) operad in sets is the data of
Definition of an operad
A (nonsymmetric) operad in sets is the data of
An operad morphism `P \to P'` is a collection of maps `\{P(n) \to P'(n)\}_{n \geq 0}` compatible with the respective compositions and units.
One can define operads not only in sets, but also in vector spaces (algebraic operad),
in topological spaces (topological operad) and more generally in every symmetric monoidal category.
 Algebra over an operad
One of the main interest of working with operads is that they allow to encode algebraic structures through the notion of algebras over an operad.
An algebra over a certain algeraic operad `P` is the data of a vector space `X` and an operad morphism ` P \to End_X` .
In other words, this corresponds to the data of morphisms ` X \otimes \cdots \otimes X \to X`, for each `f \in P(n)`, which are concrete representations of these operations.
Example. Let `K` be a field.
For all `n \geq 0`, we consider linear maps `\nu_n : K^n \to K` defined by `(x_1, \cdots,x_n) \mapsto x_1 \cdots x_n`.
There exists an algebraic operad denoted `uAs`, such that for all `n`, the vector space `uAs(n)` is the one dimensional space generated by `\nu_n`.
Let `X` be an algebra over `uAs`. By definition, this corresponds to the data of a vector space `X` and a collection
of linear maps `\{\mu_n : X^{\otimes n} \to X \}`. In particular, there is a linear map `\mu_2 : X \otimes X \to X`.
The compositions `\mu_2 \circ_1 \mu_2` and `\mu_2 \circ_2 \mu_2` both correspond to the element `\nu_3` of `uAs(3)`
so that they coincide: `\mu_2` is associative.
Furthemore, the map `\mu_1 : X \to X` is the identity of `X` since an operad morphism preserves the unit.
The map `\mu_0 : X^0 \to X` corresponds to the choice of an element `e \in X`. The compositions
`\mu_2 \circ_1 e ` and `\mu_2 \circ_2 e` both correspond to the element `\nu_1` of `uAs(1)` and are both equal.
We deduce that `e \in X` is a left and right unit for `\mu_2`. Thus, the structure of algebra over `uAs` turns `X` into a unitary associative algebra.
Conversely, one can show that any unitary associative algebra corresponds to an algebra over `uAs`. Thus, the operad `uAs`
fully encodes the structures of unitary associative algebra. There exist equally an operad denoted `uCom` which encodes the unitary
commutative algebras, an operad `Lie` associated to Lie algebras, an operad `Pois` which encodes Poisson algebras etc.
The operadic calculus thus provides a unified framework for dealing with all algebraic structures (on sets, vector spaces, or in any other symmetric monoidal category).
It allows to compare various algebraic structures, or to apply classically known results in a certain type of algebra to other algebras, etc.
Algebra over an operad
One of the main interest of working with operads is that they allow to encode algebraic structures through the notion of algebras over an operad.
An algebra over a certain algeraic operad `P` is the data of a vector space `X` and an operad morphism ` P \to End_X` .
In other words, this corresponds to the data of morphisms ` X \otimes \cdots \otimes X \to X`, for each `f \in P(n)`, which are concrete representations of these operations.
Example. Let `K` be a field.
For all `n \geq 0`, we consider linear maps `\nu_n : K^n \to K` defined by `(x_1, \cdots,x_n) \mapsto x_1 \cdots x_n`.
There exists an algebraic operad denoted `uAs`, such that for all `n`, the vector space `uAs(n)` is the one dimensional space generated by `\nu_n`.
Let `X` be an algebra over `uAs`. By definition, this corresponds to the data of a vector space `X` and a collection
of linear maps `\{\mu_n : X^{\otimes n} \to X \}`. In particular, there is a linear map `\mu_2 : X \otimes X \to X`.
The compositions `\mu_2 \circ_1 \mu_2` and `\mu_2 \circ_2 \mu_2` both correspond to the element `\nu_3` of `uAs(3)`
so that they coincide: `\mu_2` is associative.
Furthemore, the map `\mu_1 : X \to X` is the identity of `X` since an operad morphism preserves the unit.
The map `\mu_0 : X^0 \to X` corresponds to the choice of an element `e \in X`. The compositions
`\mu_2 \circ_1 e ` and `\mu_2 \circ_2 e` both correspond to the element `\nu_1` of `uAs(1)` and are both equal.
We deduce that `e \in X` is a left and right unit for `\mu_2`. Thus, the structure of algebra over `uAs` turns `X` into a unitary associative algebra.
Conversely, one can show that any unitary associative algebra corresponds to an algebra over `uAs`. Thus, the operad `uAs`
fully encodes the structures of unitary associative algebra. There exist equally an operad denoted `uCom` which encodes the unitary
commutative algebras, an operad `Lie` associated to Lie algebras, an operad `Pois` which encodes Poisson algebras etc.
The operadic calculus thus provides a unified framework for dealing with all algebraic structures (on sets, vector spaces, or in any other symmetric monoidal category).
It allows to compare various algebraic structures, or to apply classically known results in a certain type of algebra to other algebras, etc.
 To find out more:
To find out more: