The little discs operad

Operads in topological spaces are called topological operads. The little 2-discs operad `D_2` of Boardman and Vogt is an example of such operad.

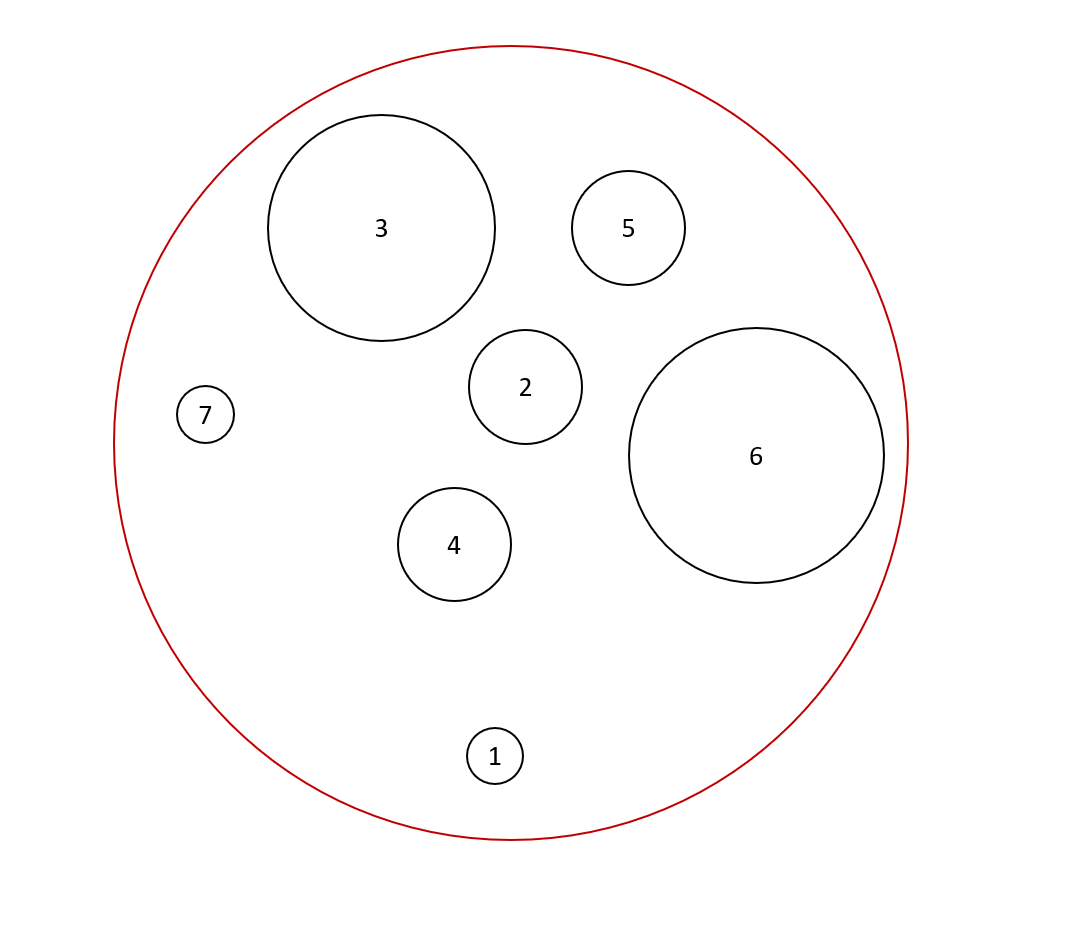
Let `n \geq 1`. We denote by `D_2(n)` the space of configurations of `n` disjoint discs inside the unit disc of dimension `2`. Every element of `D_2(n)` can be seen as a collection `\{s_1, \cdots, s_n\}`, where each `s_i` is an embedding of the circle `S^1` into the unit disc. The collection must also satisfy a non-intersection condition.

The following picture shows an element of `D_2(7)`, where the image of an embedding `s_i` is numbered by `i`.


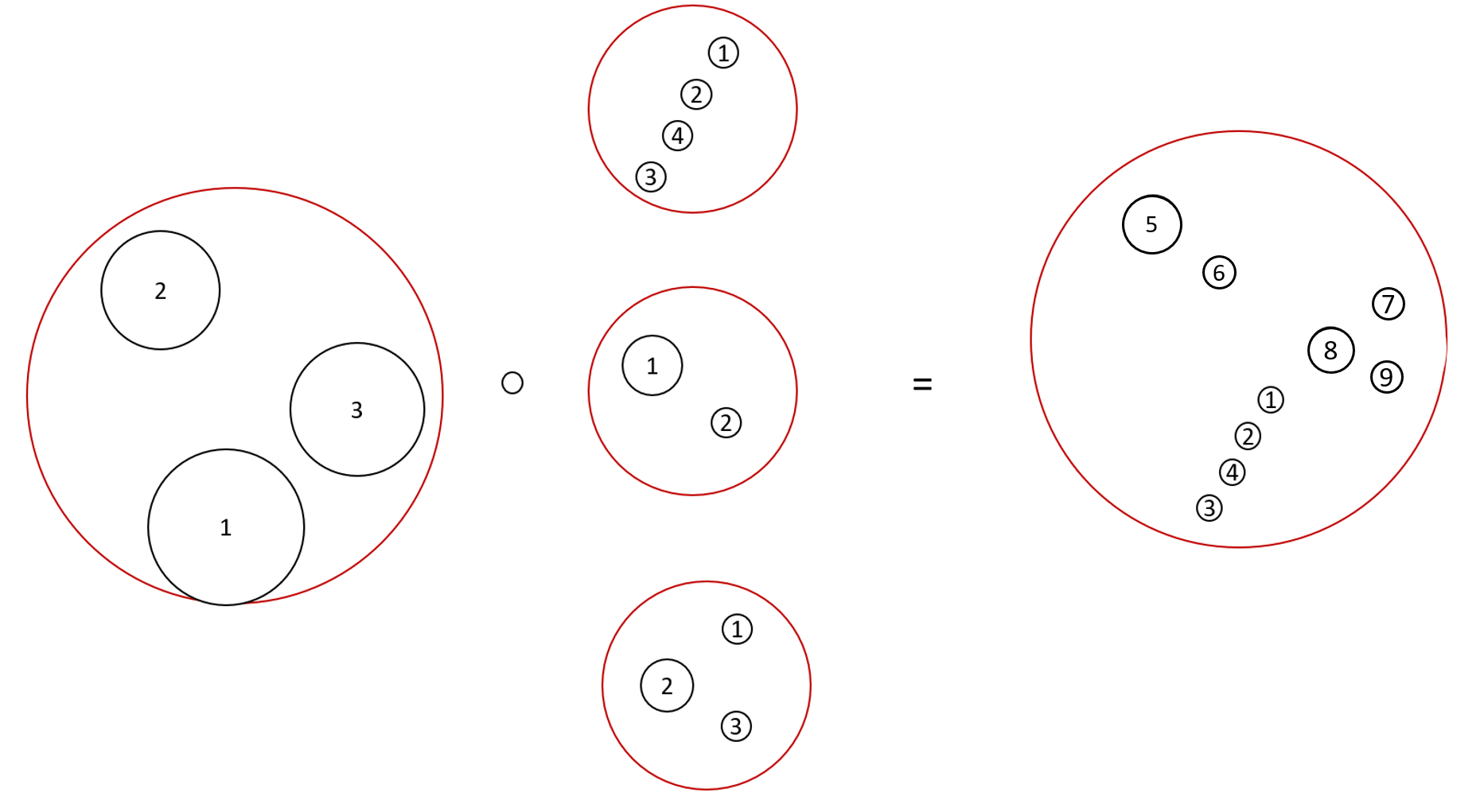
An example of composition is given by the following picture. It consists of intersecting configurations in the unit disk with the disks of a first configuration.


One can generalize this construction for all `k \geq 2` and define the operad `D_k` of little `k`-discs. The space `D_k(n)` corresponds for all `n \geq 1` to the space of configurations of `n` disjoint discs in the unit disc of dimension `k`.