| Home |
Research
|
 |
| Home |
Research
|
 |
Operads were introduced in algebraic topology in the early 1970s, in order to recognize iterated loop spaces.
The original definition is due to Peter May and was given in his book (The Geometry of Iterated Loop Spaces).
He describes an operad as a set of operations endowed with a notion of composition and subject to various conditions.
 Loop spaces
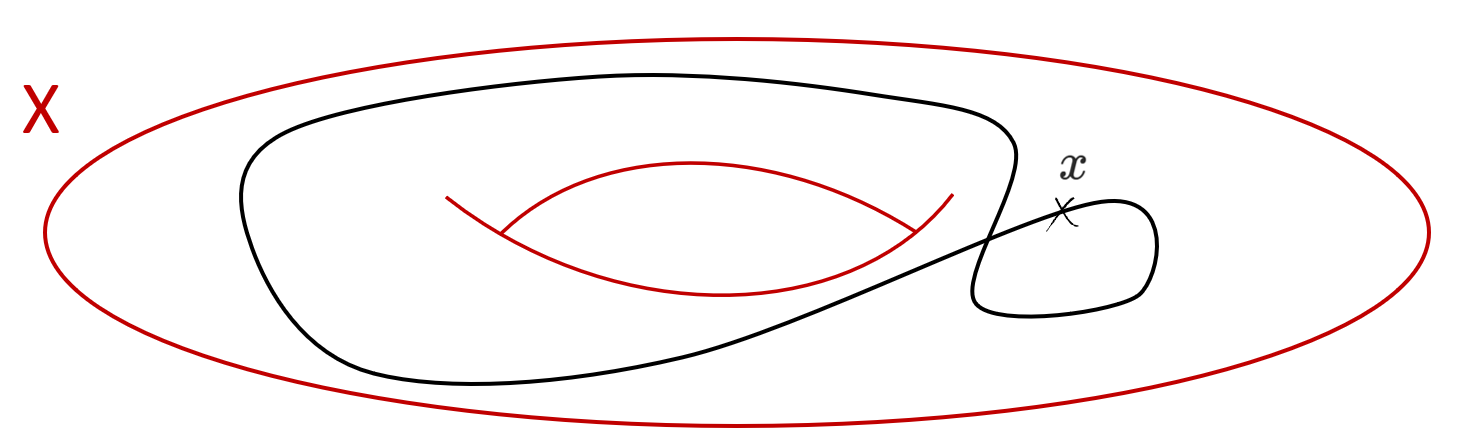
Let `X` be a topological space and `x\in X` a choice of base point.
A loop in `X` is a path in this space which starts and ends at the base point `x`. Formally, one can see a loop as a map from the interval `[0,1]`
to `X` which sends `0` and `1` to `x`. Equivalently, it is also a map from the circle `S^1` to `X` which sends the north Pole to `x`.
The following picture depicts a loop in a torus.
Loop spaces
Let `X` be a topological space and `x\in X` a choice of base point.
A loop in `X` is a path in this space which starts and ends at the base point `x`. Formally, one can see a loop as a map from the interval `[0,1]`
to `X` which sends `0` and `1` to `x`. Equivalently, it is also a map from the circle `S^1` to `X` which sends the north Pole to `x`.
The following picture depicts a loop in a torus.
 We denote by `\Omega X` the space of loops in `X`. Given two loops `f` and `g` in `\Omega X`, they can be concatenated,
i.e. one can first go through the loop `f` and then through `g` . This leads to a third loop denoted `(f , g)` .
It corresponds to the map `[0,1] \to X` defined by `f(t)` if `t \leq 1/2`
and ` g(t)` otherwise. We depict it by the following picture.
We denote by `\Omega X` the space of loops in `X`. Given two loops `f` and `g` in `\Omega X`, they can be concatenated,
i.e. one can first go through the loop `f` and then through `g` . This leads to a third loop denoted `(f , g)` .
It corresponds to the map `[0,1] \to X` defined by `f(t)` if `t \leq 1/2`
and ` g(t)` otherwise. We depict it by the following picture.
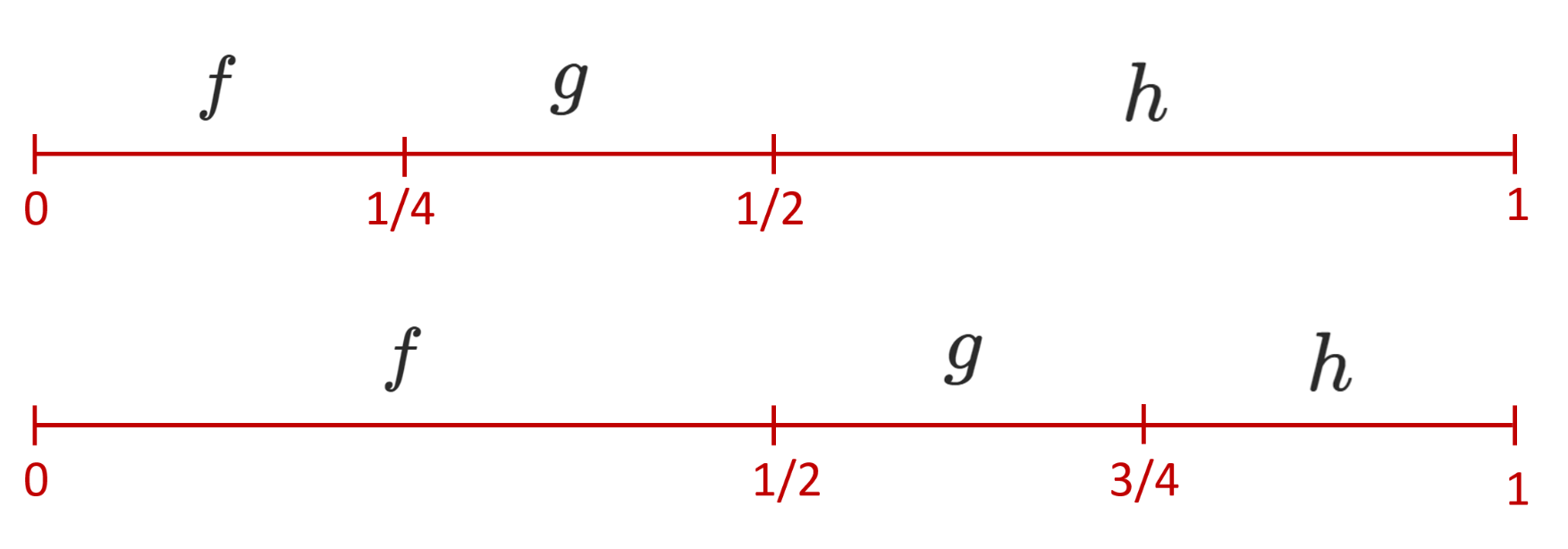
 We get a binary operation `\Omega X \times \Omega X \to \Omega X` which is not associative.
Indeed, let `h` be a third loop. Then, the concatenations `( (f , g),h) ` and `(f, (g,h))`
are not equal and correspond to two different parameterizations of the interval `[0,1]`:
We get a binary operation `\Omega X \times \Omega X \to \Omega X` which is not associative.
Indeed, let `h` be a third loop. Then, the concatenations `( (f , g),h) ` and `(f, (g,h))`
are not equal and correspond to two different parameterizations of the interval `[0,1]`:
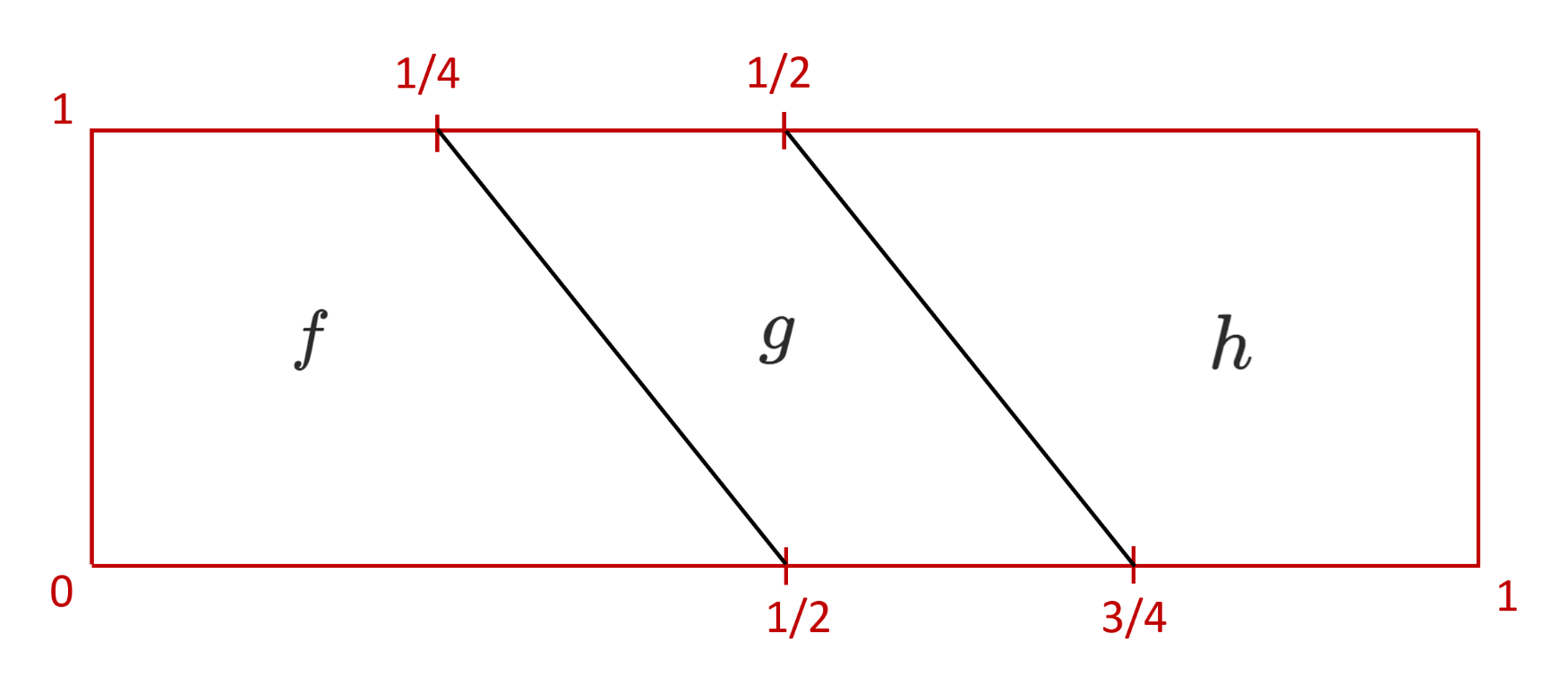
 However, there is a map `H : [0,1] \times [0,1] \to X` called homotopy, which allows to pass from one to the other,
that is, such that `H(-, 0) = ( f , (g, h) )` and `H(-, 1) = ( (f , g),h)`. It is depicted by the following picture.
However, there is a map `H : [0,1] \times [0,1] \to X` called homotopy, which allows to pass from one to the other,
that is, such that `H(-, 0) = ( f , (g, h) )` and `H(-, 1) = ( (f , g),h)`. It is depicted by the following picture.
 With this homotopy `H` the concatenation of loops is almost associative. We say that the concatenation is associative up to homotopy.
One may wonder what happens if we concatenate not three but four laces.
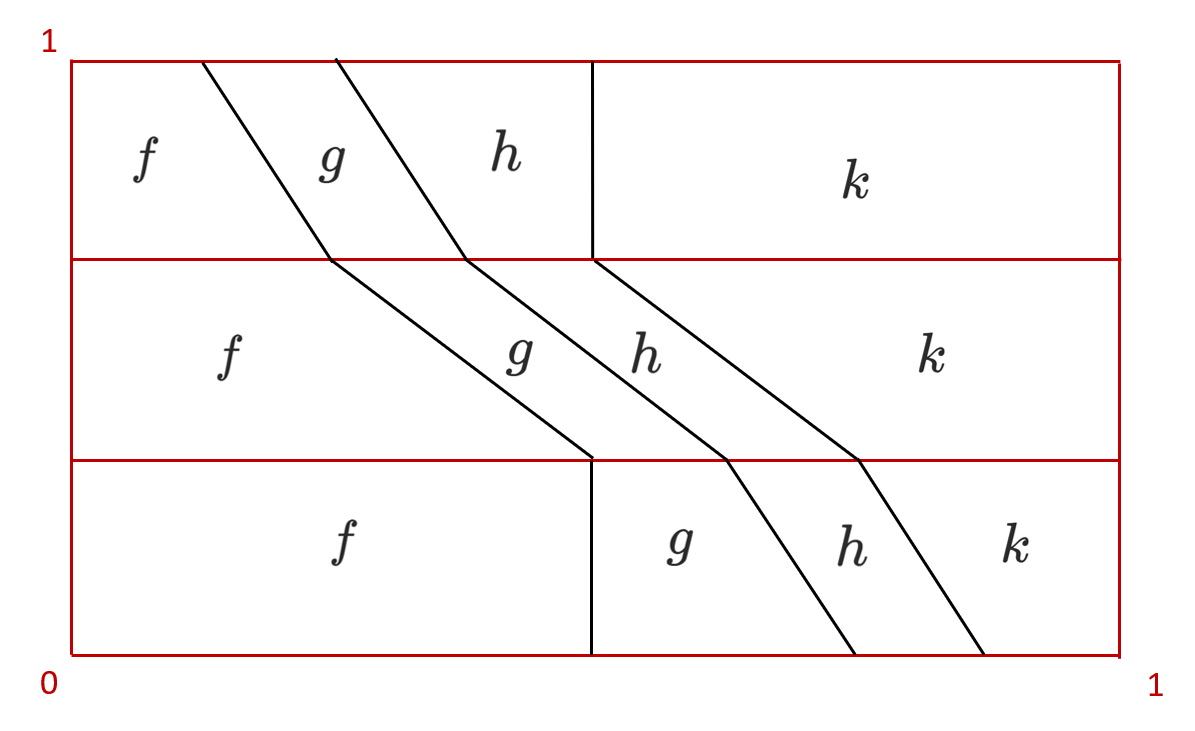
Let `k` be a loop in `X`. We have a homotopy that comes from the composition of three successive homotopies,
`H_1 : (((f,g),h),k) \to ((f,(g,h)),k) \to (f,((g,h),k)) \to (f,(g,(h,k))) `, depicted by the following picture.
With this homotopy `H` the concatenation of loops is almost associative. We say that the concatenation is associative up to homotopy.
One may wonder what happens if we concatenate not three but four laces.
Let `k` be a loop in `X`. We have a homotopy that comes from the composition of three successive homotopies,
`H_1 : (((f,g),h),k) \to ((f,(g,h)),k) \to (f,((g,h),k)) \to (f,(g,(h,k))) `, depicted by the following picture.
 However, we have a second way to connect `(((f,g),h),k)` to `(f,(g,(h,k)))` by a homotopy given by
`H_2 : (((f,g),h),k) \to ``(``(f,g),(h,k)) \to (f,(g,(h,k))) `.
It turns out that once again, one can find a homotopy between `H_1` and `H_2` !
Iterating this process, we see that the concatenation is associative up to homotopy, with homotopies between these homotopies, and homotopies between
those, and so on. As depicted in the previous pictures, we can encode each way of composing `k` loops as an embedding
of `k` copies of the interval `[0,1]` into itself.
More generally, for all `n`, one can define the `n`th iterated loop space of `X`, denoted `\Omega^n X`. It is the space of all maps from the unit sphere
`S^n` to `X` which sends the north Pole to `x`.
As before, we can define the composition of iterated loops and encode the ways of composing `k` iterated loops
in `\Omega^n X` as embeddings of `k` copies of `[0,1]^n` into itself. The concatenation is again associative up to homotopy,
with homotopies between these homotopies, ect.
However, we have a second way to connect `(((f,g),h),k)` to `(f,(g,(h,k)))` by a homotopy given by
`H_2 : (((f,g),h),k) \to ``(``(f,g),(h,k)) \to (f,(g,(h,k))) `.
It turns out that once again, one can find a homotopy between `H_1` and `H_2` !
Iterating this process, we see that the concatenation is associative up to homotopy, with homotopies between these homotopies, and homotopies between
those, and so on. As depicted in the previous pictures, we can encode each way of composing `k` loops as an embedding
of `k` copies of the interval `[0,1]` into itself.
More generally, for all `n`, one can define the `n`th iterated loop space of `X`, denoted `\Omega^n X`. It is the space of all maps from the unit sphere
`S^n` to `X` which sends the north Pole to `x`.
As before, we can define the composition of iterated loops and encode the ways of composing `k` iterated loops
in `\Omega^n X` as embeddings of `k` copies of `[0,1]^n` into itself. The concatenation is again associative up to homotopy,
with homotopies between these homotopies, ect.
 How to encode this entire structure?
The question that arises is how to properly encode all these structures and in particular the data of the different homotopies.
The existence of higher homotopies between different ways of composing the loops amounts to ensuring that each of the corresponding embeddings are contractible.
May proved the following theorem:
Theorem. For all `n`, there exists an operad `C_n` in topological spaces, encoding embeddings of copies of
`[0,1]^n` into itself, such that every loop space `\Omega^n X` is a `C_n`-algebra.
Conversely, if a connected topological space `Y` is a `C_n`-algebra, then it is weakly homotopy equivalent to an iterated loop space under the form `\Omega^n X`.
How to encode this entire structure?
The question that arises is how to properly encode all these structures and in particular the data of the different homotopies.
The existence of higher homotopies between different ways of composing the loops amounts to ensuring that each of the corresponding embeddings are contractible.
May proved the following theorem:
Theorem. For all `n`, there exists an operad `C_n` in topological spaces, encoding embeddings of copies of
`[0,1]^n` into itself, such that every loop space `\Omega^n X` is a `C_n`-algebra.
Conversely, if a connected topological space `Y` is a `C_n`-algebra, then it is weakly homotopy equivalent to an iterated loop space under the form `\Omega^n X`.
 To find out more :
To find out more :
