| Accueil |
Recherche
|
 |
| Accueil |
Recherche
|
|
Les opérades sont des outils qui permettent d'encoder des structures algébriques. On peut voir une opérade comme une classe d’opérations
abstraites, munies d'une certaine façon cohérente de les composer.
L'opérade des endomorphismes
Pour comprendre la définition formelle d'une opérade, on s'intéresse à l'exemple fondamental de l'opérade des endomorphismes.
Soit `X` un ensemble. On note `End_X(n):= Hom(X^{n}, X)` l'ensemble des applications du produit de `n` copies de `X` vers `X`.
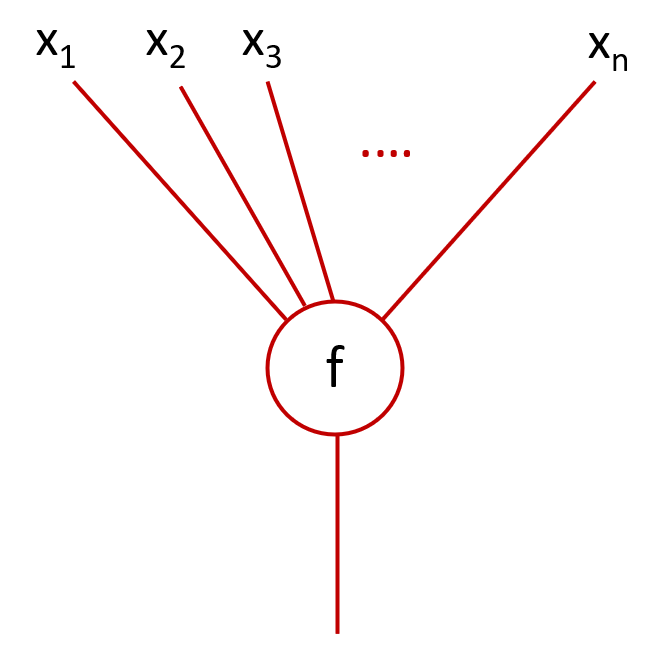
On peut penser aux éléments de `End_X(n)`, comme à des arbres où le nombre de feuilles correspond aux arguments de `f` et la racine à la sortie.
La figure suivante représente une application ` f : X^{ n} \to X` d'arité `n`.
Étant données deux applications `f : X^{ n} \to X` et `g : X^{ m} \to X` , il existe une façon évidente de les composer en
remplaçant une des entrées de `f` par la racine de `g` . En choisissant par exemple la deuxième entrée de `f`, on obtient
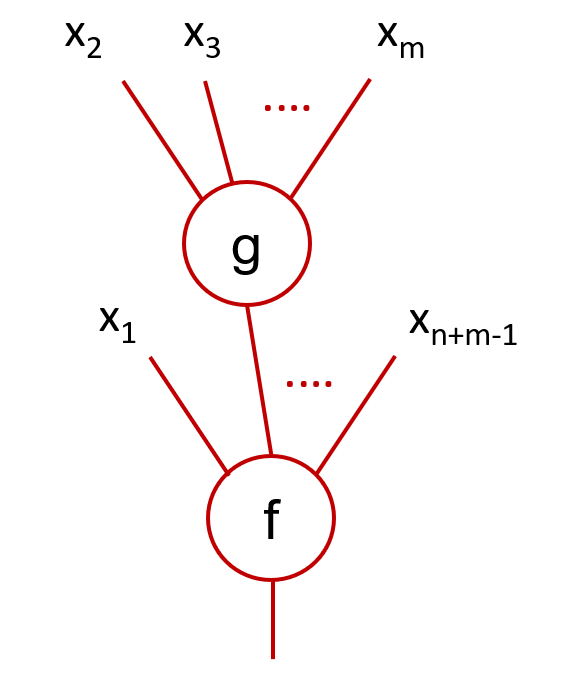Cette composition correspond à la formule `f(x_1,g(x_2, \cdots, x_m), \cdots, x_{n+m-1})`, pour `x_1, \cdots, x_{n+m-1} \in X`.
On la note `f \circ_2 g`. On a remplacé la deuxième entrée de `f` mais on peut tout aussi bien choisir la `i`-ème entrée, pour
chaque `i \in \{1, \cdots, n \}`. Cela donne lieu à une composition que l'on note `f \circ_i g`.
Si l'on compose plusieurs applications de cette façon, l'ordre des compositions n'importe pas.
En d'autre termes, les compositions sont associatives. Par exemple, si l'on se donne une troisième application `h : X^{ p} \to X`,
on a `(f \circ_2 g) \circ_4 h = f \circ_2 (g \circ_3 h)` ou encore `(f \circ_2 g) \circ_{n+m-2} h = (f \circ_{n-1} h) \circ_2 g` .
Ainsi, les deux exemples de compositions représentés par les figures suivantes ne sont pas ambiguës.
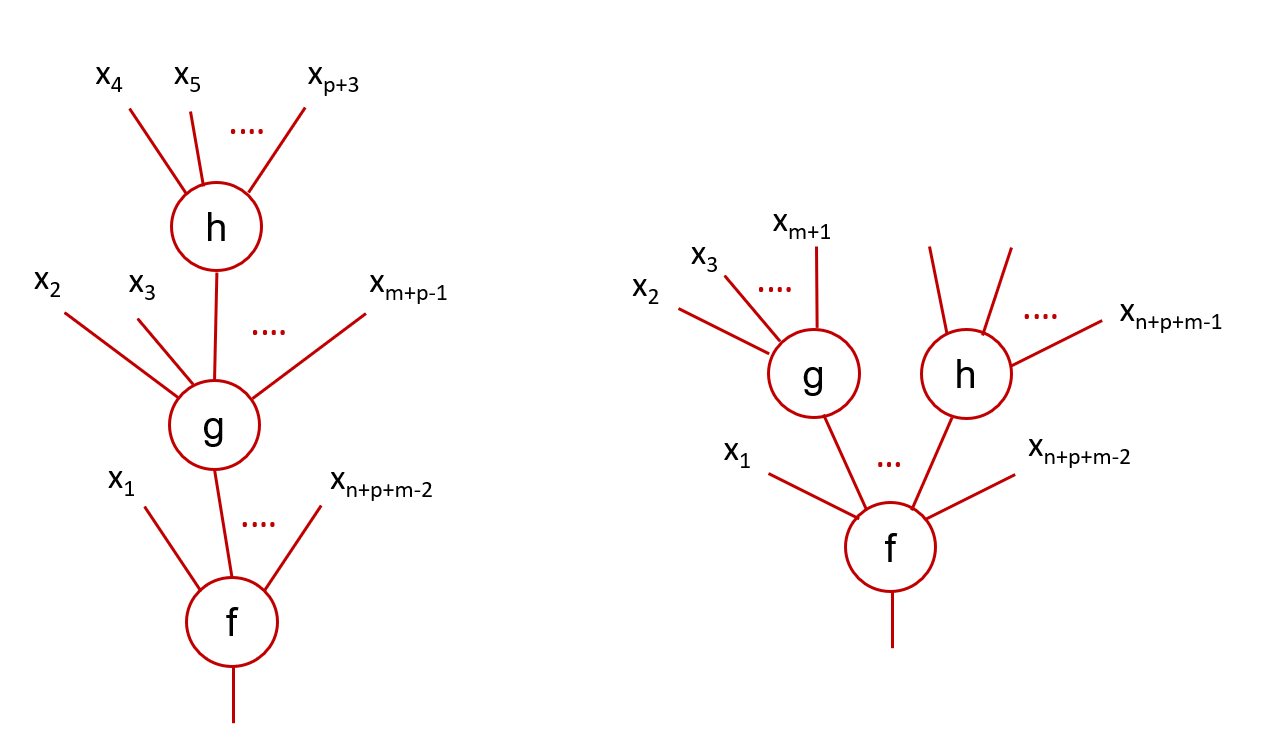On parle respectivement de composition séquentielle dans le cas de l'arbre de gauche et de
composition parallèle dans celui de l'arbre de droite.
L'application `id_X \in End_X(1)` est un élément neutre, c'est-à-dire que pour tout `f : X^{ n} \to X` et `i \in \{1, \cdots, n \}` , la composition
`f \circ_i id_X ` est égale à `f` . De même, on a `id_X \circ_1 f =f` .
On peut également autoriser des applications `X^{ 0} \to X` d'arité `0` . L'espace `X^{ 0}` est simplement un singleton
et toute application `X^{ 0} \to X` est entièrement déterminée par la donnée d'un élément `a \in X`. On a ainsi un isomorphisme `End_X(0) \cong X`.
On représente ces applications d'arité `0` comme des bouchons :
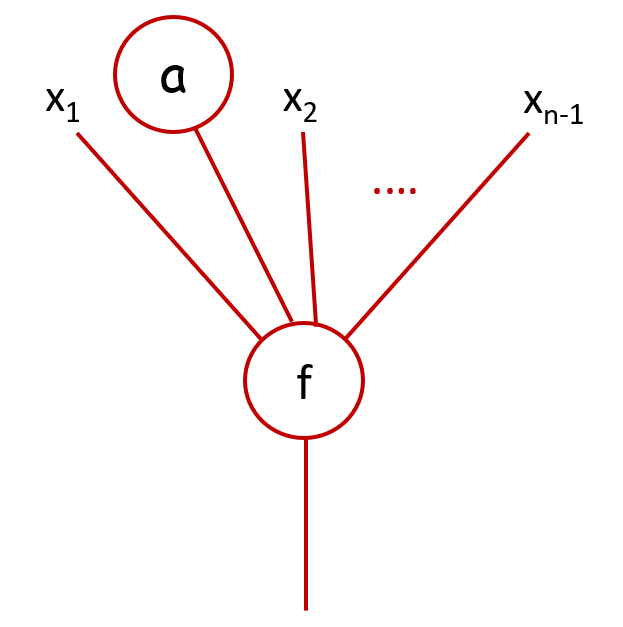
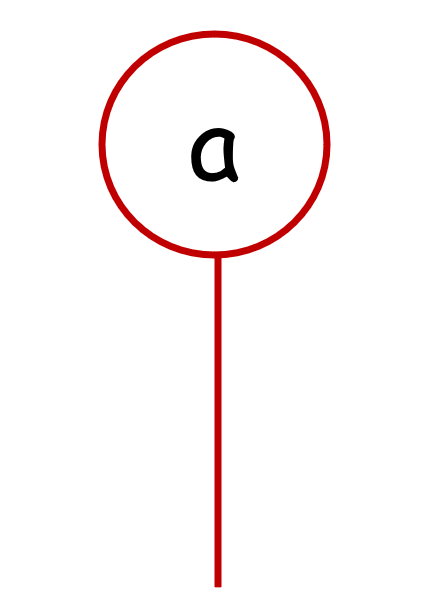Si `f` est une application `X^{n} \to X` où `n \geq 1`, la composition `f \circ_i a` pour `i \in \{1, \cdots, n \}` de `f` avec un bouchon `a \in End_X(0)`
revient à bloquer l'entrée `i` de `f` en la forçant à être égale à `a` . Avec la représentation en arbres, on obtient la figure suivante pour `f \circ_2 a`
qui correspond à la formule `f(x_1,a,x_2, \cdots, x_{n-1})`, pour `x_1, \cdots, x_{n-1} \in X`.
On peut à présent donner la définition d'une opérade.
Définition d'une opérade
Une opérade (non-symétrique) dans la catégorie des ensembles est la donnée
Un morphisme d'opérades `P \to P'` est une collection d'applications `\{P(n) \to P'(n)\}_{n \geq 0}` compatibles avec les compositions et les unités respectives.
Notons que l'on peut définir une opérade non seulement dans les ensembles, mais aussi dans les espaces vectoriels (on parle d'opérade algébrique),
dans les espaces topologiques (on parle d'opérade topologique) et plus généralement dans n'importe quelle catégorie symétrique
monoïdale.
Algèbre sur une opérade
L'un des principaux intérets des opérades est qu'elles permettent d'encoder des structures algébriques à travers la notion d'algèbre sur une opérade.
Une algèbre sur une opérade algébrique `P` est la donnée d'un espace vectoriel `X` et d'un morphisme d'opérades ` P \to End_X` .
En d'autres termes, il s'agit de la donnée de morphismes ` X \otimes \cdots \otimes X \to X`, pour chaque opération `f \in P(n)`, qui sont des
réalisations concrètes de ces opérations.
Exemple. Soit `K` un corps fixé.
Pour tout `n \geq 0`, on considère l'application linéaire `\nu_n : K^n \to K` définie par `(x_1, \cdots,x_n) \mapsto x_1 \cdots x_n`.
Il existe une opérade algébrique notée `uAs` telle que pour tout `n`, l'espace vectoriel `uAs(n)` est l'espace de dimension `1` engendré par `\nu_n`.
Soit `X` une algèbre sur `uAs`. Par construction, la donnée d'une telle algèbre correspond à un espace vectoriel `X`
munit pour tout `n` d'une application `\mu_n : X^{\otimes n} \to X`. En particulier, on a une application linéaire
`\mu_2 : X \otimes X \to X`. Les compositions `\mu_2 \circ_1 \mu_2` et `\mu_2 \circ_2 \mu_2`
correspondent toutes les deux à l'élément `\nu_3` de `uAs(3)` et sont donc égales : `\mu_2` est associative.
De plus, l'application `\mu_1 : X \to X` est l'identité de `X` puisque un morphisme d'opérades préserve l'unité.
L'application `\mu_0 : X^0 \to X` correspond au choix d'un élément `e \in X`. Les compositions
`\mu_2 \circ_1 e ` et `\mu_2 \circ_2 e` correspondent toutes les deux à
l'élément `\nu_1` de `uAs(1)` et sont donc égales. On en déduit que `e \in X` est une unité à gauche
et à droite pour `\mu_2` et que la structure d'algèbre sur `uAs` fait de `X` une algèbre associative unitaire.
Réciproquement, on peut montrer que toute algèbre associative unitaire correspond à une algèbre sur `uAs`. De fait, l'opérade `uAs`
encode complètement la structure d'algèbre associative unitaire. Il existe également une opérade notée `uCom` qui encode les algèbres commutatives unitaires, une opérade `Lie` associée aux algèbres
de Lie, une opérade `Pois` qui encode les algèbres de Poisson etc.
Le langage opéradique fournit ainsi un cadre unifié pour traiter toutes les structures algébriques (sur des ensembles, des espaces vectoriels, ou dans toute autre catégorie monoïdale symétrique).
Il permet de comparer différentes structures algébriques, ou encore d’appliquer des résultats classiquement connus dans le cadre d'un certain type d’algèbre à d’autres algèbres, etc.
Pour en savoir plus