| Accueil |
Recherche
|
 |
| Accueil |
Recherche
|
 |
Les opérades ont été introduites en topologie algébrique au début des années 1970, notamment pour reconnaître les espaces de lacets itérés.
La définition originelle est dûe à Peter May et a été donnée dans son livre (The Geometry of Iterated Loop Spaces).
Il y décrit une opérade comme un ensemble d’opérations dotées d’une notion de composition et soumises à diverses conditions.
 Espace de lacets
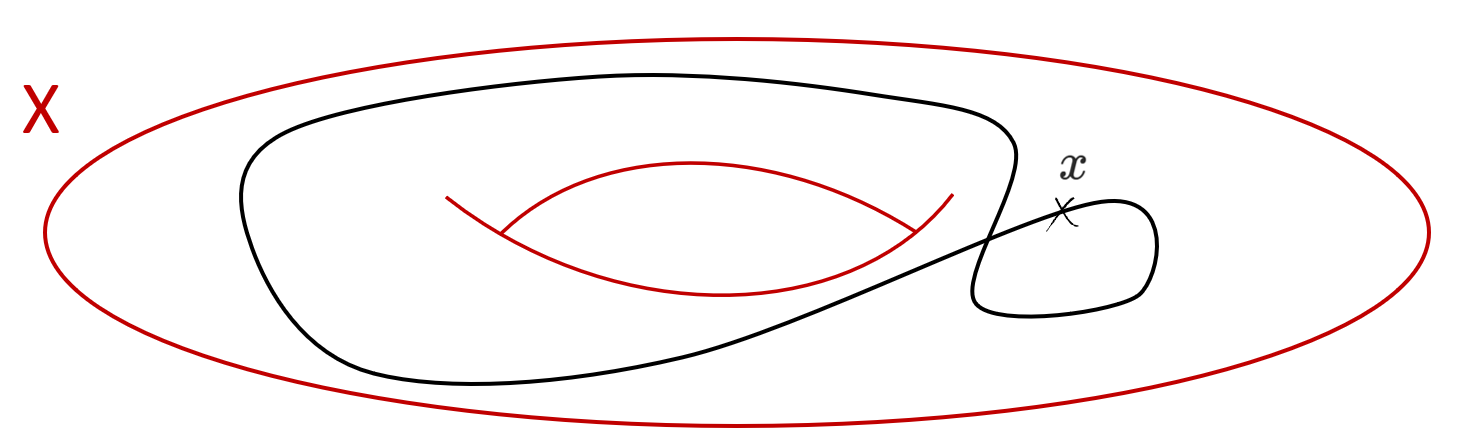
Soient `X` un espace topologique et `x\in X` un point de base.
Un lacet dans `X` est un chemin dans cet espace qui part du point de base `x` et qui revient
au point de départ. Formellement, on peut voir un lacet comme une application de l'intervalle `[0,1]`
dans `X` telle que les images de `0` et de `1` soient `x`. De façon équivalente, il s'agit d'une application du cercle `S^1` dans `X`
qui envoie le pôle nord sur `x`.
La figure suivante représente un exemple de chemin sur un tore.
Espace de lacets
Soient `X` un espace topologique et `x\in X` un point de base.
Un lacet dans `X` est un chemin dans cet espace qui part du point de base `x` et qui revient
au point de départ. Formellement, on peut voir un lacet comme une application de l'intervalle `[0,1]`
dans `X` telle que les images de `0` et de `1` soient `x`. De façon équivalente, il s'agit d'une application du cercle `S^1` dans `X`
qui envoie le pôle nord sur `x`.
La figure suivante représente un exemple de chemin sur un tore.
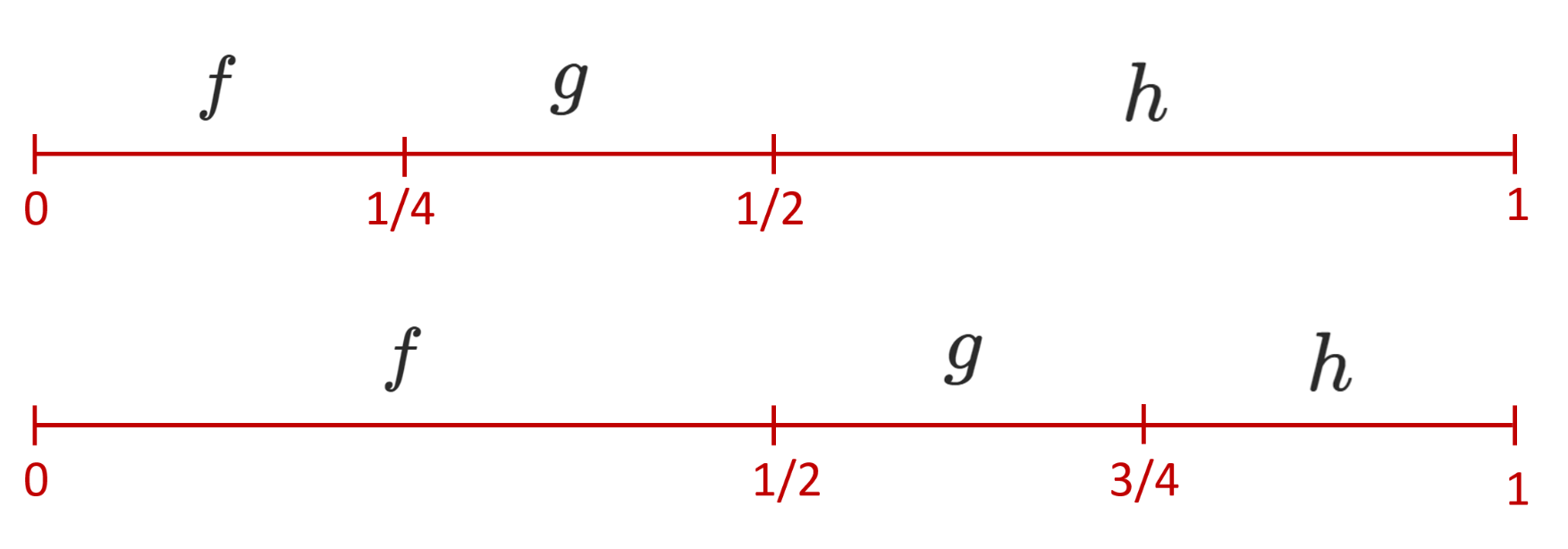
 On note `\Omega X` l'espace des lacets de `X`. Lorsque l'on se donne deux lacets `f` et `g` dans `\Omega X`, on peut les
concaténer, c'est-à-dire parcourir d'abord le lacet `f` puis le lacet `g` . Cela donne lieu à un troisième
lacet, noté `(f , g)`, qui correspond à l'application `[0,1] \to X` définie par `f(t)` si `t \leq 1/2`
et ` g(t)` sinon. On le représente par la figure suivante.
On note `\Omega X` l'espace des lacets de `X`. Lorsque l'on se donne deux lacets `f` et `g` dans `\Omega X`, on peut les
concaténer, c'est-à-dire parcourir d'abord le lacet `f` puis le lacet `g` . Cela donne lieu à un troisième
lacet, noté `(f , g)`, qui correspond à l'application `[0,1] \to X` définie par `f(t)` si `t \leq 1/2`
et ` g(t)` sinon. On le représente par la figure suivante.
 On obtient une opération binaire `\Omega X \times \Omega X \to \Omega X` qui n'est pas associative.
En effet, soit `h` un troisième lacet. Alors les concaténations `( (f , g),h) ` et `(f, (g,h))`
ne sont pas égales et correspondent à deux paramétrisations de l'intervalle `[0,1]` différentes:
On obtient une opération binaire `\Omega X \times \Omega X \to \Omega X` qui n'est pas associative.
En effet, soit `h` un troisième lacet. Alors les concaténations `( (f , g),h) ` et `(f, (g,h))`
ne sont pas égales et correspondent à deux paramétrisations de l'intervalle `[0,1]` différentes:
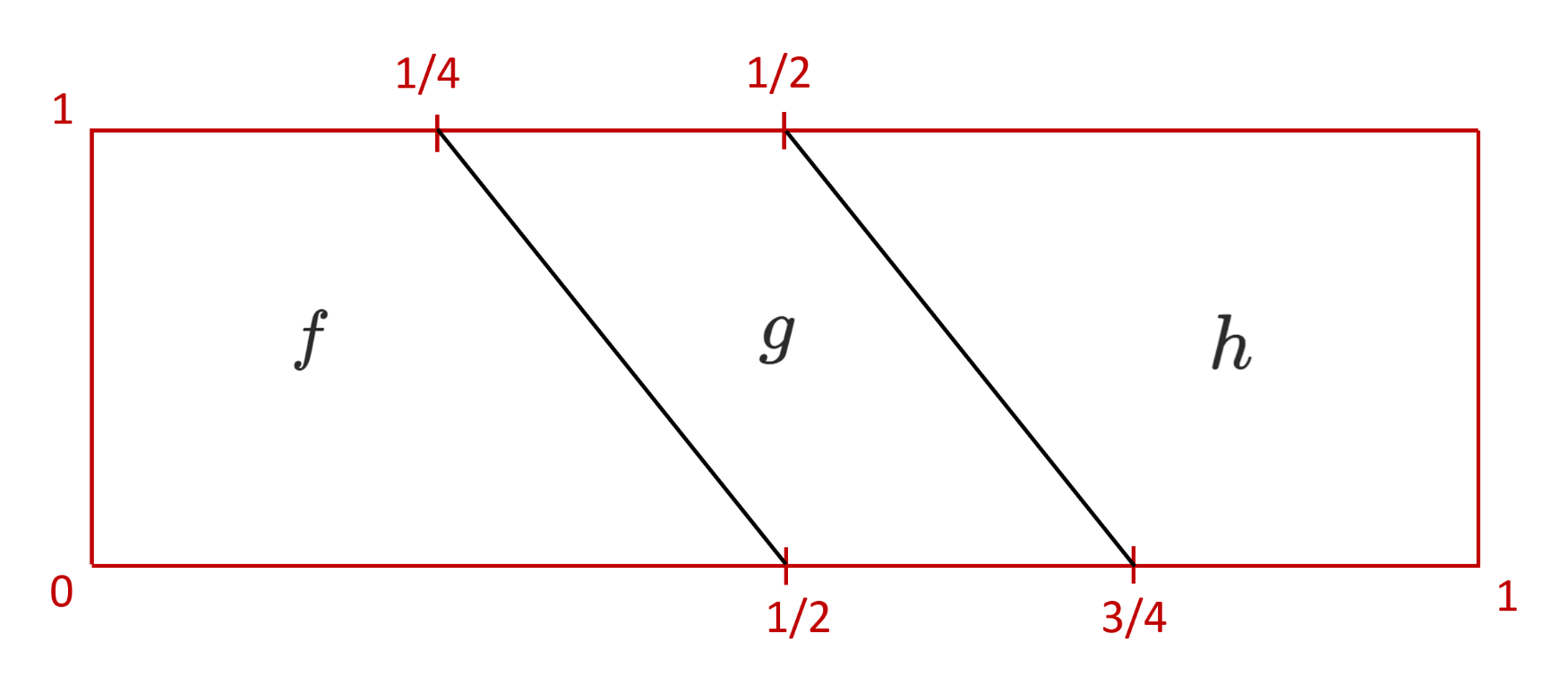
 En revanche, il existe une application `H : [0,1] \times [0,1] \to X` qualifiée d'homotopie qui permet de passer de l'une à l'autre,
c'est-à-dire telle que `H(-, 0) = ( f , (g, h) )` et `H(-, 1) = ( (f , g),h)`. Elle est représentée par la figure suivante.
En revanche, il existe une application `H : [0,1] \times [0,1] \to X` qualifiée d'homotopie qui permet de passer de l'une à l'autre,
c'est-à-dire telle que `H(-, 0) = ( f , (g, h) )` et `H(-, 1) = ( (f , g),h)`. Elle est représentée par la figure suivante.
 Moyennant cette homotopie `H` la concaténation des lacets est associative. On dit que la concaténation est associative à homotopie près.
On peut se demander ce qu'il se passe si l'on cherche à concaténer non plus trois mais quatre lacets.
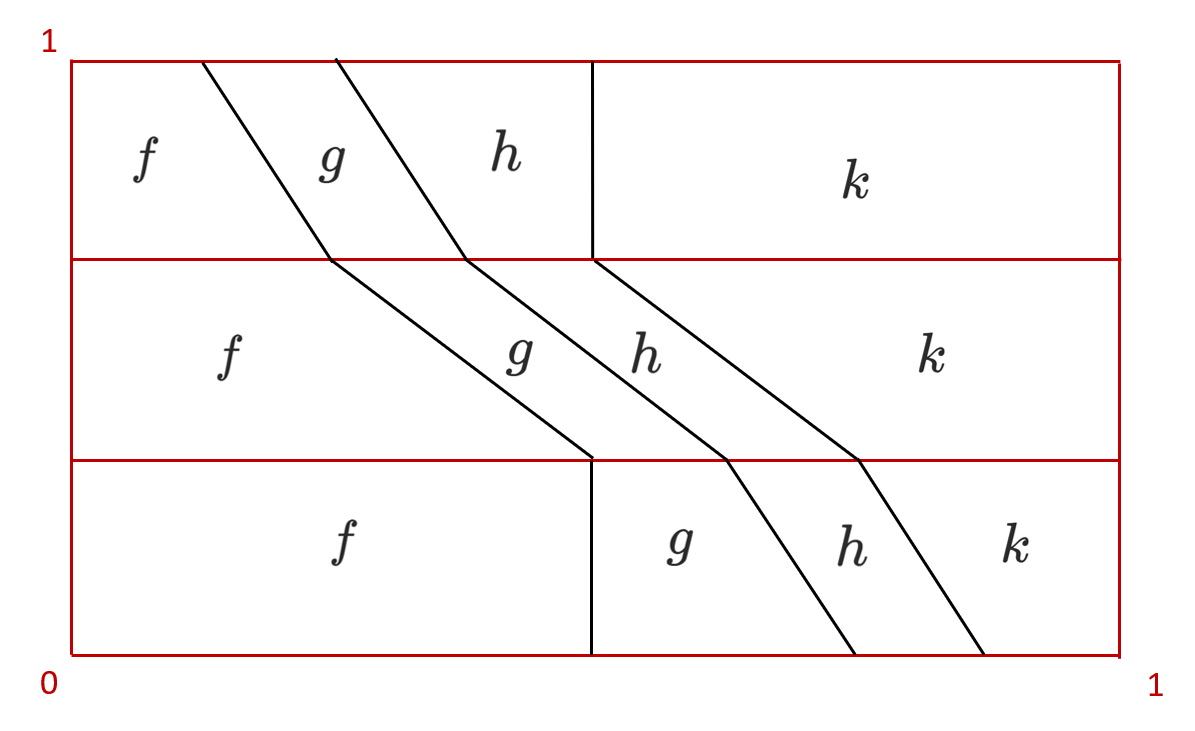
Soit `k` un lacet de `X`. On a une homotopie qui provient de la composition de trois homotopies successives,
`H_1 : (((f,g),h),k) \to ((f,(g,h)),k) \to (f,((g,h),k)) \to (f,(g,(h,k))) ` représentée par la figure suivante.
Moyennant cette homotopie `H` la concaténation des lacets est associative. On dit que la concaténation est associative à homotopie près.
On peut se demander ce qu'il se passe si l'on cherche à concaténer non plus trois mais quatre lacets.
Soit `k` un lacet de `X`. On a une homotopie qui provient de la composition de trois homotopies successives,
`H_1 : (((f,g),h),k) \to ((f,(g,h)),k) \to (f,((g,h),k)) \to (f,(g,(h,k))) ` représentée par la figure suivante.
 On a cependant une deuxième façon de relier `(((f,g),h),k)` à `(f,(g,(h,k)))` par une homotopie donnée par
`H_2 : (((f,g),h),k) \to ``(``(f,g),(h,k)) \to (f,(g,(h,k))) `.
Il s'avère qu'une fois encore, on peut trouver une homotopie entre `H_1` et `H_2` !
En itérant ce processus, on voit que la concaténation est associative à homotopies près, avec des homotopies entre ces homotopies, et des homotopies entre
celles-ci, et ainsi de suite. Comme on l'a représenté dans les figures précédentes, on peut encoder chacune des manières de composer `k` lacets comme un
plongement de `k` copies de l'intervalle `[0,1]` dans `[0,1]`.
Plus généralement, pour tout entier `n`, on définit le `n`-ième espace de lacets itérés de `X`, noté `\Omega^n X`, comme l'espace des applications de la sphère unité `S^n` dans `X` qui envoient le pôle nord sur `x`.
De la même façon que précédemment, on peut définir la composition de lacets itérés et encoder les manières de composer `k` lacets
itérés dans `\Omega^n X` comme un plongement de `k` copies de `[0,1]^n` dans lui-même. La concaténation est encore associative
à homotopies près, avec des homotopies entre ces homotopies, ect.
On a cependant une deuxième façon de relier `(((f,g),h),k)` à `(f,(g,(h,k)))` par une homotopie donnée par
`H_2 : (((f,g),h),k) \to ``(``(f,g),(h,k)) \to (f,(g,(h,k))) `.
Il s'avère qu'une fois encore, on peut trouver une homotopie entre `H_1` et `H_2` !
En itérant ce processus, on voit que la concaténation est associative à homotopies près, avec des homotopies entre ces homotopies, et des homotopies entre
celles-ci, et ainsi de suite. Comme on l'a représenté dans les figures précédentes, on peut encoder chacune des manières de composer `k` lacets comme un
plongement de `k` copies de l'intervalle `[0,1]` dans `[0,1]`.
Plus généralement, pour tout entier `n`, on définit le `n`-ième espace de lacets itérés de `X`, noté `\Omega^n X`, comme l'espace des applications de la sphère unité `S^n` dans `X` qui envoient le pôle nord sur `x`.
De la même façon que précédemment, on peut définir la composition de lacets itérés et encoder les manières de composer `k` lacets
itérés dans `\Omega^n X` comme un plongement de `k` copies de `[0,1]^n` dans lui-même. La concaténation est encore associative
à homotopies près, avec des homotopies entre ces homotopies, ect.
 Comment encoder l'ensemble de cette structure ?
La question qui se pose est de comment bien conserver l'ensemble de ces structures et notamment la donnée des différentes homotopies.
L'existence d'homotopies supérieures entre différentes manières de composer les lacets revient à s'assurer que chacun des
plongements correspondants sont contractiles. May a alors démontré le théorème suivant :
Théorème. Pour tout `n`, il existe une opérade `C_n` dans les espaces topologiques
qui encode les plongements de copies de l'intervalle `[0,1]^n` dans lui-même, et telle que chaque espace de lacets itéré `\Omega^n X` est une `C_n`-algèbre.
Réciproquement, si un espace connexe `Y` est une `C_n`-algèbre alors il est homotopiquement faiblement équivalent à un espace de lacets de la forme `\Omega^n X`.
Comment encoder l'ensemble de cette structure ?
La question qui se pose est de comment bien conserver l'ensemble de ces structures et notamment la donnée des différentes homotopies.
L'existence d'homotopies supérieures entre différentes manières de composer les lacets revient à s'assurer que chacun des
plongements correspondants sont contractiles. May a alors démontré le théorème suivant :
Théorème. Pour tout `n`, il existe une opérade `C_n` dans les espaces topologiques
qui encode les plongements de copies de l'intervalle `[0,1]^n` dans lui-même, et telle que chaque espace de lacets itéré `\Omega^n X` est une `C_n`-algèbre.
Réciproquement, si un espace connexe `Y` est une `C_n`-algèbre alors il est homotopiquement faiblement équivalent à un espace de lacets de la forme `\Omega^n X`.
 Pour en savoir plus
Pour en savoir plus
