L'opérade des petits disques

Les opérades dans les espaces topologiques sont qualifiées d'opérades topologiques. Un exemple paradigmatique d’une telle opérade est l'opérade `D_2` des petits 2-disques de Boardman et Vogt.

Soit `n \geq 1`, on note `D_2(n)` l'espace topologique des configurations de `n` disques disjoints dans le disque unité du plan noté `D`. Un élément de `D_2(n)` est entièrement déterminé par la donné de `n` applications continues `s_i` du cercle `S^1` vers `D` pour `i \in \{1, \cdots, n\}`, satisfaisant une condition de non-intersection. Le disque correspondant à l'image de l'application `s_i` sera numéroté `i`.

La figure suivante présente un élément de `D_2(7)`.


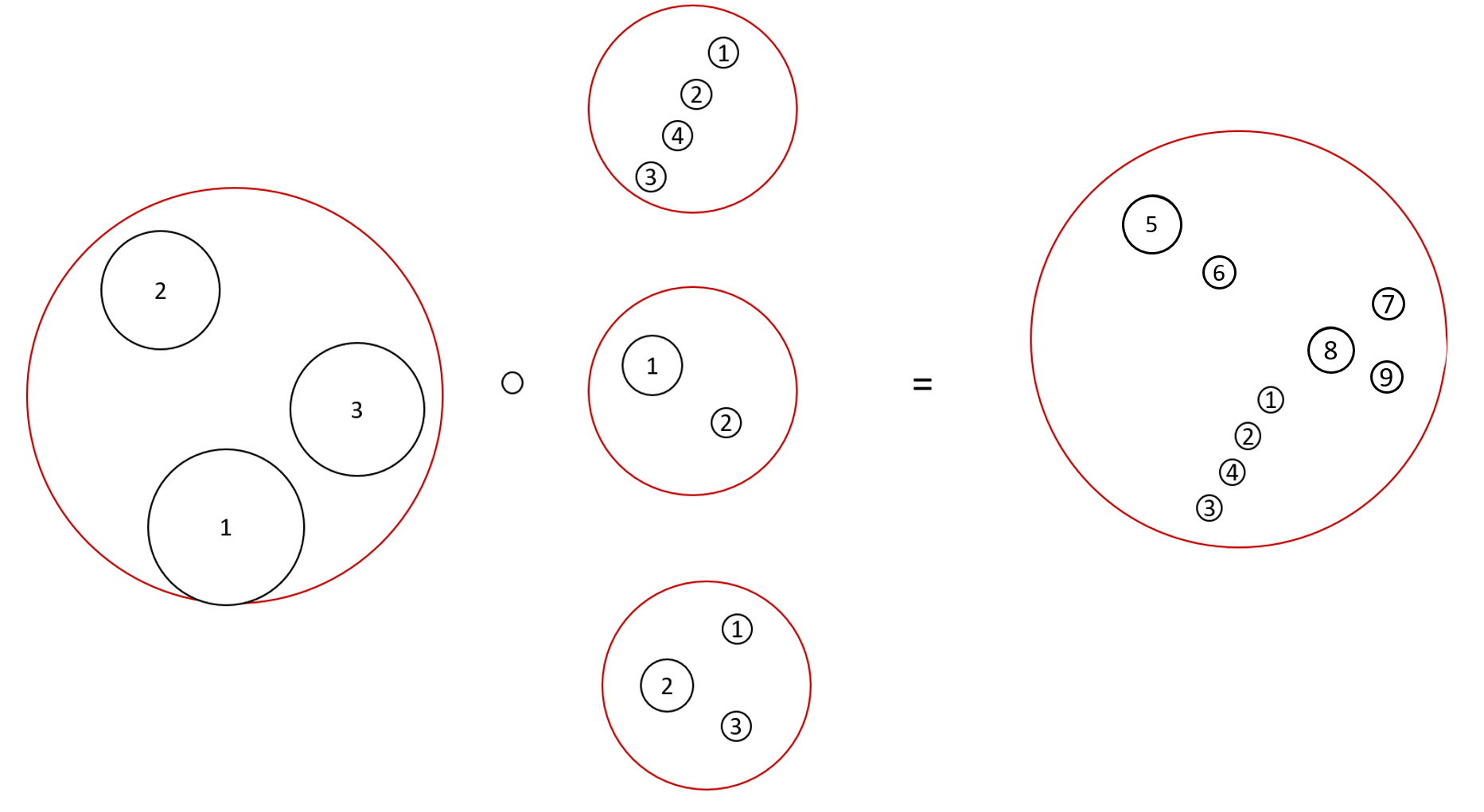
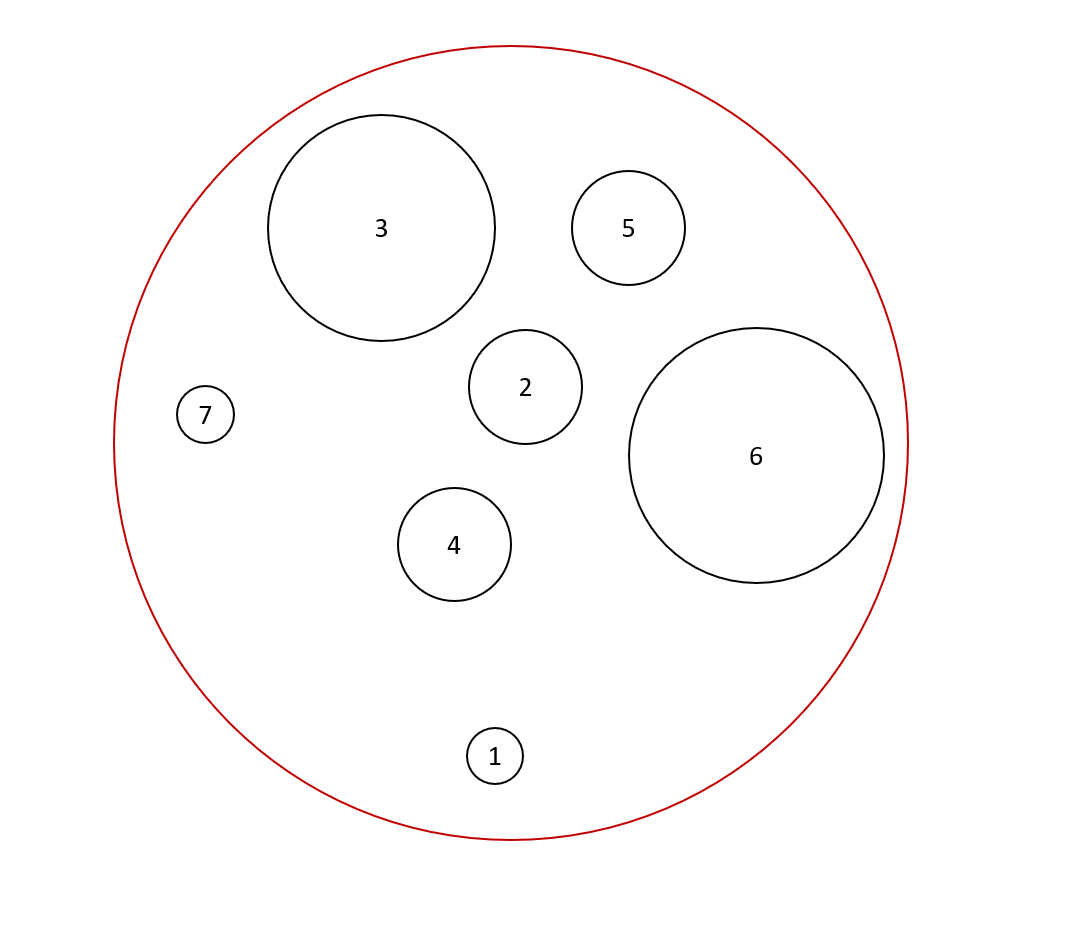Les compositions sont illustrées par la figure suivante. Elles consistent à intersecter des configurations dans le disque unité avec les disques d'une première configuration.


On peut généraliser cette construction pour tout entier `k \geq 2` et définir l'opérade `D_k` des petits `k`-disques, où `D_k(n)` correspond pour `n \geq 1` à l'espace topologique des configurations de `n`-disques disjoints dans le disque unité de l'espace réel `R^k`.